Теорема Лапласа о разложении определителя по элементам строки (столбца)

Определители любого порядка возможно вычислить по теореме Лапласа.

Теорема Лапласа: определитель квадратной матрицы равен сумме произведений элементов любой строки или столбца на их алгебраические дополнения (разложение по элементам какого – либо ряда)

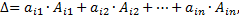
где -алгебраические дополнения элементов строк матрицы. Или

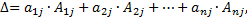
где 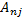-алгебраические дополнения элементов столбцов матрицы.

Алгебраическим дополнением 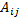элемента определителя называется его минор, взятый со своим знаком, если сумма индексов 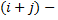число четное, и с противоположным знаком, если сумма индексов ( 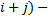число нечетное

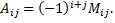
Найдем алгебраическое дополнение для элемента 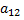матрицы

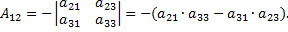
Каждая матрица n-го порядка имеет 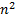миноров -го порядка.

Найдем алгебраические дополнения для элементов первой строки матрицы

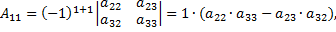
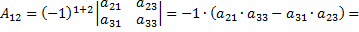
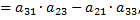
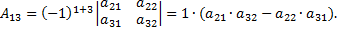
Запишем определитель матрицы и вычислим с помощью разложения по первой строке

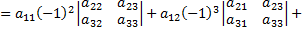
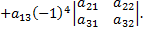
Аналогично можно разложить определитель матрицы по любой строке или столбцу.

Рассмотрим пример.

Вычислим определитель, разложив его по первой строке

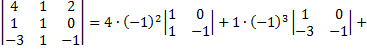
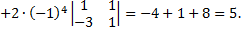
Вычислим определитель, разложив его по второму столбцу

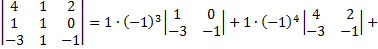
Основные свойства определителей.

1) При транспонировании матрицы ее определитель не меняется

2) Если в матрице поменять местами два столбца или две строки, то знак определителя поменяется на противоположный, а абсолютная величина останется прежней.

3) Определитель с одинаковыми столбцами равен нулю.

4) Общий множитель элементов столбца (или строки) можно вынести за знак определителя

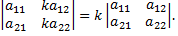
5) Если в определителе есть столбец, в котором все элементы равны нулю, то определитель равен нулю.

6) Определитель не изменится, если к элементам столбца прибавить соответствующие элементы другого столбца, умноженные на одно и то же число.

Контрольные вопросы

1. Дать определение матрицы, пояснить нумерацию элементов. Как определить размер или порядок матрицы?

2. Как сложить (вычесть) матрицы, умножить на число?

3. Какие действия с матрицами называют линейными?

4. Перечислить свойства линейных операций.

5. Сформулировать правило умножения матриц.

6. Перечислить свойства произведения матриц.

7. Дать определение минора 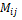элемента определителя.

8. Перечислить основные свойства определителей.