Определители второго и третьего порядков и их свойства
Пусть А - произвольная квадратная матрица n-го порядка 

Определителем квадратнойматрицы n-го порядка называется число, которое может быть вычислено по элементам матрицы

где  -минор элемента определителя.
-минор элемента определителя.
Минором 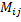 элемента определителя называется определитель, который получится, если в исходном определителе вычеркнуть строку и столбец, на пересечении которых находится данный элемент
элемента определителя называется определитель, который получится, если в исходном определителе вычеркнуть строку и столбец, на пересечении которых находится данный элемент 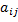 .
.
Следует обратить внимание на то, что определители имеют только квадратные матрицы, т.е. матрицы, у которых число строк равно числу столбцов.
Формула, которая позволяет вычислить определитель матрицы по первой строке
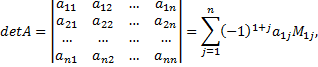
где 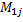 -определитель квадратной матрицы, полученной из матрицы
-определитель квадратной матрицы, полученной из матрицы  вычеркиванием первой строки и j-го столбца.
вычеркиванием первой строки и j-го столбца.
Обозначение 
Для определителей второго и третьего порядка легко получить выражения через элементы матрицы.
Определитель второго порядка:

Определитель третьего порядка:


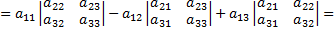


Порядок матрицы является и порядком определителя.
Вычисление определителей второго порядка
Например:

Вычисление определителей третьего порядка.
Определители третьего порядка можно вычислить по правилу треугольника
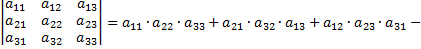
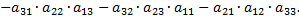
Рассмотрим пример:
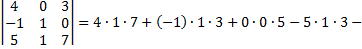
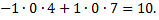
Дата добавления: 2015-08-11; просмотров: 1503;
