Понятие о решении системы линейных алгебраических уравнений

Система линейных уравнений с переменными имеет вид

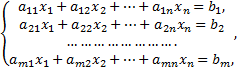
где 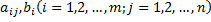-произвольные числа, называемые соответственно коэффициентами при переменных и свободными членами уравнений.

В более краткой записи с помощью знаков суммирования систему можно записать в виде

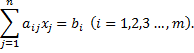
Решением системы линейных уравнений называется такая совокупность чисел, при подстановке которых каждое уравнение системы обращается в верное равенство.

Система уравнений называется совместной, если она имеет хотя бы одно решение, и несовместной, если она не имеет решений.

Совместная система уравнений называется определенной, если она имеет единственное решение, и неопределенной, если она имеет более одного решения.

Рассмотрим пример. Система уравнений

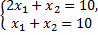
- совместная и определенная, так как имеет единственное решение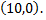

Система

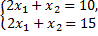
- несовместная.

Система

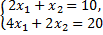
- совместная и неопределенная, так как имеет более одного, а точнее бесконечное множество решений 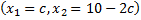, за 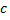принимается любое число.

Две системы уравнений называются равносильными, или эквивалентными, если они имеют одно и то же множество решений.