Матричная запись системы линейных алгебраических уравнений и ее решение методом обратной матрицы
Матричный метод решения систем линейных алгебраических уравнений:
- применим к решению систем линейных алгебраических уравнений, где число уравнений равно числу неизвестных;
- удобен для решения систем линейных алгебраических уравнений невысокого порядка;
Определим операцию деления матриц, как операцию, обратную умножению.
Пусть дана система
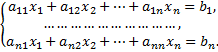
Составим матрицы
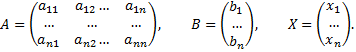
Пусть матрица A –невырожденная.
Систему уравнений можно записать в следующем виде

Умножим обе части матричного уравнения на обратную матрицу

получили решение матричного уравнения.
В развернутом виде

Выполнив умножение матриц, запишем решение системы.
Для применения данного метода необходимо найти обратную матрицу, что может быть связано с вычислительными трудностями при решении систем высокого порядка.
Рассмотрим пример. Решить систему матричным способом
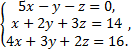
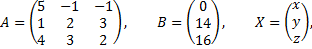
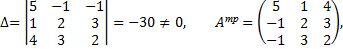
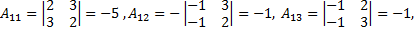

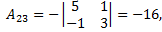
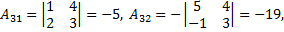
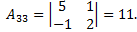
Тогда
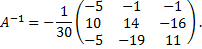
Следовательно,
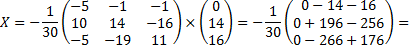
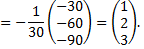
Дата добавления: 2015-08-11; просмотров: 1438;
