Алгоритм обратной матрицы

Опишем алгоритм применительно к решению ЗЛП, записанной в канонической форме с односторонними ограничениями:

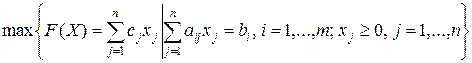
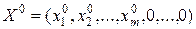Пусть известен начальный опорный план с базисом 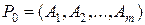, т.е. 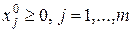- базисные компоненты, 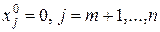- небазисные компоненты.

В данном методе все параметры итерации, необходимые для оценки плана на оптимальность и перехода к лучшему плану, вычисляются через элементы 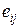обратной матрицы 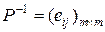. Поэтому второй алгоритм симплекс-метода также называют алгоритмом обратной матрицы.

Вычисления удобно выполнять, используя две симплекс-таблицы:

Основная таблица

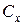
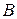
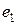
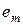
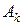
№		P			…			t
					…			…
…	…	…	…	…	…	…	…	…
					…
…	…	…	…	…	…	…	…	…
					…			…
					…

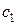
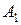
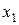
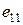
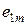
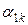
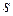
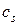
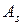
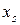
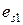
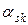
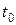
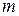
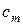
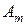
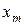
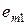
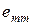
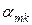
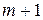
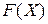
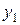
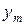
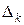
Вспомогательная таблица

№			…
			…
…	…	…	…	…
			…
			…
			…
			…
			…
…	…	…	…	…

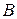
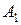
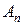
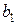
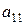
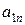
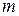
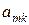
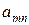
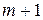
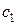
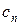
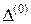
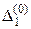
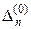
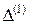
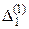
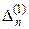
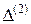
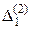
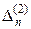
Порядок вычислений по второму алгоритму

Шаг 1. Найти обратную матрицу 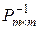и заполнить её элементами 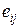столбцы 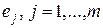, основной симплекс-таблицы.

Шаг 2. Вычислить значение линейной формы 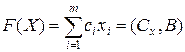как скалярное произведение столбцов 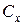и 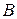основной таблицы. Результат занести в 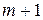строку столбца 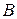основной симплекс-таблицы.

Шаг 3. Вычислить значения элементов вектора-строки 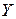по формуле 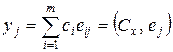, как скалярное произведение столбцов 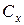и 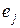основной симплекс-таблицы. Полученными значениями заполнить 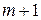-ю строку основной симплекс-таблицы.

Шаг 4. Найти значения оценок 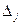векторов условий 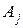относительно базиса по формуле 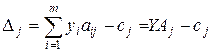, , 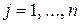как произведение вектора-строки 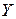основной таблицы на соответствующий столбец 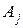вспомогательной таблицы минус соответствующий коэффициент 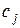линейной формы, записанный в 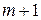-ой строке вспомогательной таблицы. Полученные значения занести в строку вспомогательной таблицы с номером, соответствующим номеру выполняемой итерации.

Шаг 5. Проверить оптимальность опорного плана.

· Если все оценки неотрицательные ( 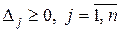), то 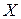- оптимальный опорный план и, тогда, в столбце 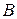основной симплекс-таблицы записано решение ЗЛП, а именно, значения базисных компонент оптимального опорного плана и соответствующее ему максимальное значение линейной формы. На этом процесс решения ЗЛП завершается.

· Если среди оценок найдутся отрицательные ( 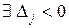), то для построения нового опорного плана необходимо найти вектор, который будет вводиться в базис. Он определяется по номеру наименьшей отрицательной оценки 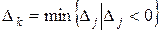и, таким образом, устанавливается разрешающий столбец .

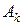Шаг 6. Вычислить коэффициенты разложения 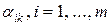вектора 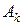по базису 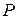, используя формулу 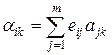, как произведение 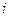-ой строки обратной матрицы 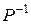из основной таблицы на столбец 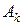вспомогательной таблицы. Полученные значения занести в столбец 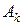основной симплекс-таблицы.

Шаг 7. Определить вектор, выводимый из базиса. Для этого необходимо заполнить столбец 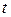основной таблицы значениями 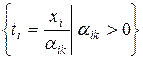путем деления элементов столбца основной таблицы на соответствующие им по номеру элементы столбца 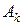основной таблицы.

· Если все 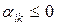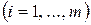, то исходная задача неразрешима в силу неограниченности сверху линейной формы 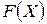. На этом процесс решения ЗЛП завершается.

· Если 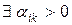, то необходимо выбрать 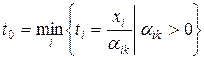. Пусть им оказался элемент с номером 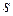, т.е. 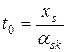. Тогда соответствующий этому индексу 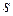вектор 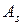должен выводиться из базиса. Элемент 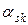является «разрешающим». На этом нулевая итерация завершена и надлежит приступить к выполнению следующей итерации.

Шаг 8.Для заполнения новой основной таблицы вычислить по рекуррентным формулам новые значения параметров итерации.

· Заполнить 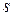-тую строку новой основной таблицы элементами 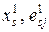, , 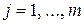получающимися делением соответствующих элементов ( 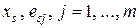) 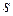-той строки старой основной таблицы на разрешающий элемент 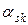, т.е. по формулам .

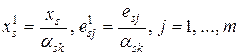· Все остальные 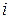-тые строки главной части новой основной симплекс-таблицы получить как результат вычитания из 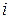-той строки старой основной симплекс-таблицы 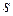-той строки новой симплекс-таблицы, умноженной на соответствующий 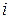-тый элемент разрешающего столбца 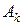старой основной симплекс-таблицы, т.е. в соответствии с рекуррентными формулами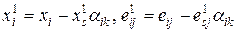 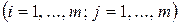. По аналогичным формулам могут быть вычислены также и элементы 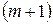-й строки: .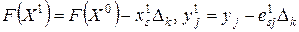

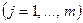Описанный процесс построения симплекс-таблиц повторяется до получения оптимального опорного плана или до установления неограниченности линейной формы, т.е. неразрешимости ЗЛП.