О конечности симплекс - метода

Пусть ЗЛП является невырожденной. Тогда на каждом шаге симплекс – метода будем иметь 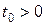. Процесс расчета будет состоять в переходе

,

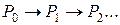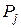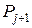где два соседних базиса отличаются лишь одним вектором. Например, переход от к осуществлен введением вектора 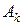. При этом линейная форма изменится так:

,

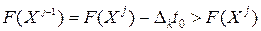т.к. 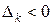и .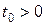

Таким образом, при переходе от одного опорного плана к другому в невырожденной задаче линейная форма возрастает. Поэтому невозможен возврат к старому опорному плану, т.е. каждый шаг симплекс – метода приводит к новому, ранее не встречавшемуся, опорному плану. И поскольку число опорных планов (вершин многогранного множества ) конечно, то в невырожденной задаче через конечное число шагов либо устанавливается неограниченность линейной формы, либо получается оптимальный план.

Пусть ЗЛП является вырожденной. Тогда у вырожденного опорного плана может быть (но не обязательно) и поэтому может быть .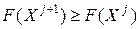

Не приведет ли это к бесконечному числу шагов? В силу конечности числа вершин множества это может быть лишь тогда, когда через несколько шагов мы вернемся к исходному базису. Следовательно, должны встречаться цепочки

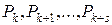
в которых начальное и конечное звенья совпадают, т.е. . Такие цепочки называются циклами. Для них 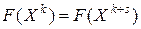. Но так как любые соседние опорные планы доставляют значение линейной формы 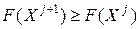, то, очевидно,

.

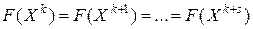Таким образом, цикл означает переход от одного базиса опорного плана к другому базису того же вырожденного опорного плана. Причем, через некоторое число таких переходов имеет место возвращение к ранее встретившемуся базису. В случае образования цикла, т.е. зацикливания, всегда можно выйти из него, специальным образом выбрав «разрешающий элемент».

Методы построения начального опорного плана

Алгоритм построения начального опорного плана

Метод последовательного улучшения плана, который применяется для решения ЗЛП, предполагает знание некоторого исходного опорного плана. Однако, далеко не всегда такой начальный опорный план может быть указан без каких-либо вычислений. Это возможно лишь в случае, когда среди столбцов 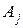матрицы условий найдётся достаточное количество таких столбцов, из которых составится единичная матрица и эта матрица будет являться базисом искомого начального плана.

Если же такой возможности нет, то для построения начального опорного плана ЗЛП решается вспомогательная ЗЛП (так называемая задача) с расширенным вектором 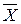, состоящим из вектора 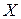исходной ЗЛП, дополненного искусственными неотрицательными компонентами 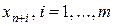. Последние вводятся в систему ограничений так, чтобы сформировался искусственный единичный базис.

Итак, начальный опорный план задачи может быть найден с помощью следующей вспомогательной ЗЛП (L - задачи):

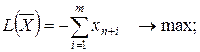
	(11.1)
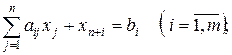
	(11.2)
	(11.3)

Так как матрица условий ЗЛП (11.1)-(11.3) уже содержит единичную подматрицу 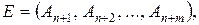которая может быть взята в качестве базиса опорного плана, то начальным опорным планом этой задачи будет являться вектор

,

у которого небазисные компоненты 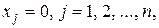а базисные .

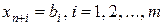Решая сформулированную задачу, например, первым алгоритмом симплекс - метода, с указанным начальным планом 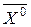, в силу ограниченности линейной формы 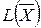сверху на множестве своих планов ( 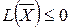) окажется, что процесс решения через конечное шагов приведет к оптимальному опорному плану вспомогательной задачи.

Пусть 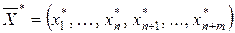- оптимальный опорный план задачи, у которого все искусственные компоненты равны нулю. Тогда вектор 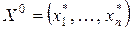является опорным планом исходной задачи. Действительно, все дополнительные переменные 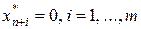. Значит, компоненты вектора 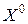удовлетворяют ограничениям исходной задачи, т.е. вектор 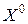является некоторым планом исходной задачи. По построению план 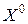является также опорным.