Анализ направленных ответвителей с помощью метода симметрии

Направленные ответвители образуют обширный класс укрупненных базовых элементов, используемых как при построении разветвленных трактов СВЧ, так и в различных измерительных устройствах. Напомним, что направленным ответвителем называют реактивный восьмиполюсник, имеющий две пары идеально согласованных и взаимно развязанных входов. Большинство направленных ответвителей имеет плоскость симметрии и поэтому подбор номиналов входящих в них элементов и анализ получающихся матриц рассеяния может производиться методом симметричного и антисимметричного возбуждения

.

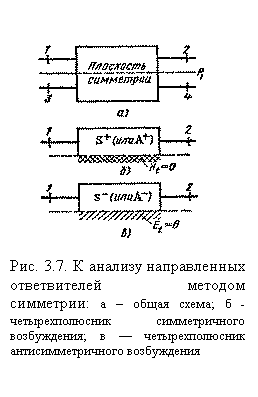
Введем нумерацию входов восьмиполюсника, показанную на рис. 3.7,а. В соответствии с формулами (2.74) и (2.75) матрица рассеяния восьмиполюсника при наличии плоскости симметрии 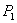должна иметь структуру:

; ;

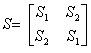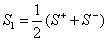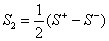
причем матрицы рассеяния второго порядка

;

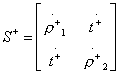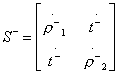
относятся к парциальным четырехполюсникам симметричного и антисимметричного возбуждения, показанным на рис. 3.7,6 и рис. 3.7, в. Эти четырехполюсники представляют собой верхние половины восьмиполюсника, отсекаемые плоскостью симметрии с граничным условием Ht=0 (симметричное возбуждение, индекс «+») или с граничным условием 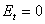(антисимметричное возбуждение, индекс «—»). Независимые между собой элементы матрицы рассеяния восьмиполюсника на рис. 3.7, а следующим образом выражаются через коэффициенты отражения 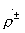и коэффициенты передачи 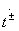парциальных четырехполюсников:

; ;

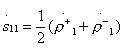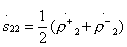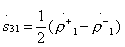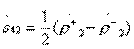; ;(3.31)

;

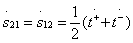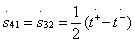
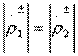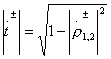причем следствием реактивности парциальных четырехполюсников являются равенства и . Реактивный восьмиполюсник на рис. 3.7,а превратится в идеальный направленный ответвитель, если будет обеспечено согласование входов 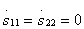и одновременно достигнута развязка каких-либо двух пар входов. В зависимости от того, между какими входами достигается развязка, различаютследующие типынаправленности: 1) типа 1 при развязке пар входов 1—3 и 2— 4;2) типа II при развязке пар входов 1—4 и 2—3;3) типа III при развязке пар входов 1— 2 и 3— 4.

Рассмотрим последовательно каждый из типов направленности.

Направленность типа 1. Совместное выполнение условий согласования входов ответвителя 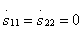и раз вязки 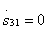согласно формулам (3.31)эквивалентно равенствам

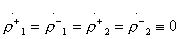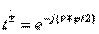; (3.32)

т. е. для достижения направленности типа 1 оба парциальных четырехполюсника симметричного и антисимметричного возбуждения должны быть идеально согласованными и отличаться лишь фазами коэффициентов передач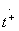и и 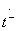. Разность фаз этих коэффициентов передачи 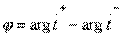называют дифференциальным фазовым сдвигом для волн, проходящих через согласованные парциальные четырехполюсники симметричного и антисимметричного возбуждения. Идеальная матрица рассеяния направленного ответвителя типа 1 при выполнении условий (3.32) имеет структуру:

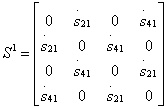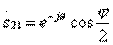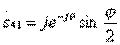; ; (3.33)

Направленные ответвители типа 1 относятся к сонаправленным ответвителям, так как волна во вторичной линии передачи 3—4 движется в ту же сторону, что и возбуждающая ее волна в первичной линии 1—2. Кроме того, направленные ответвители типа 1 являются квадратурными, т. е. фазовый сдвиг между элементам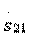и и 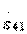в матрице рассеяния равен 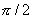. В направленном ответвителе типа 1, как правило, имеется вторая плоскость симметрии (по крайней мере электрической), проходящая между парами входов 1—3 и 2—4. Условия (3.32), определяющие направленность типа 1, могут быть переписаны в терминах классических матриц передачи 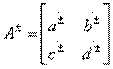для парциальных четырехполюсников. C помощью формул перехода между матрицами А и S из табл. 3.1 получаем уравнения 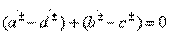, из которых с учетом вещественности элементов 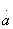и и 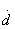мнимости элементов 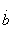и 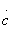в реактивном четырехполюснике следует:

направленность типа 1.(3.34)

Дифференциальный фазовый сдвиг легко определяется из соотношения ,приводящего к формуле

.

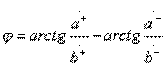Выражения для ненулевых элементов идеальной матрицы рассеяния направленного ответвителя типа 1 с учетом условий (3.34) принимают вид

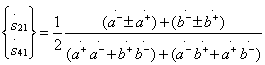(3.35)

где верхний знак относится к элементу 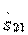, а нижний—к элементу .

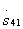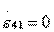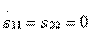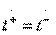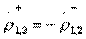2. Направленность типа II. Совместное выполнение условий развязки и согласования входов в соответствии с формулами (3.31) возможно только при выполнении равенств и . С учетом канонической матрицы рассеяния недиссипативного четырехполюсника (2.54) это приводит к выражениям

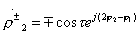; ; ,(3.36)

где 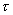, , 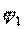— независимые вещественные параметры, определяющие матрицу рассеяния реактивного четырехполюсника.

Идеальная матрица рассеяния направленного ответвителя типа II при выполнении условий (3.36) приобретает вид:

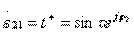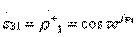; ; ;(3.37)

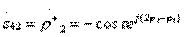
Направленные ответвители типа II относятся к противонаправленным ответвителям, так как волна во вторичной линии передачи 3—4 движется в противоположную сторону по отношению к возбуждающей ее волне в первичной линии передачи 1—2. Если направленный ответвитель типа II имеет вторую плоскость симметрии, проходящую между парами входов 1—3 и 2—4, то 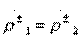, что означает 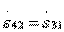и 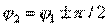. Следовательно, при наличии двух плоскостей симметрии направленный ответвитель типа II оказывается квадратурным. Если же второй плоскости симметрии нет, но подбором параметров парциальных четырехполюсников обеспечено равенство 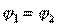, то направленный ответвитель типа II получается синфазно-противофазньм, т. е. .

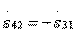Условия 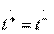, 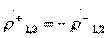определяющие направленность типа II, в терминах классических матриц передачи парциальных четырехполюсников выглядят следующим образом:

;

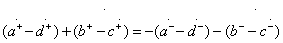
Отсюда с учетом вещественности элементов 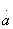и и 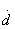мнимости элементов 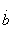и 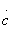в реактивных четырехполюсниках следуют условия:

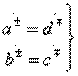направленность типа II,(3.38)

с учетом которых получаем выражения для расчета элементов идеальной матрицы рассеяния (3.37):

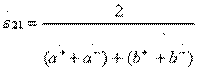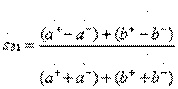; (3.39)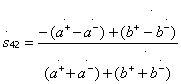

3. Направленность типа III. Совместное выполнение условий развязки 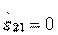и согласования входов 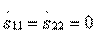в соответствии с формулами (3.31) возможно только при выполнении равенств

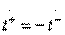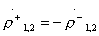; (т.е. ).

С учетом канонической матрицы рассеяния реактивного четырехполюсника эти условия принимают вид:

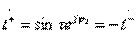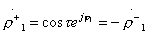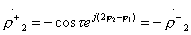; ; (3.40)

Идеальная матрица рассеяния направленного ответвителя типа III при выполнении условий (3.40) имеет структуру:

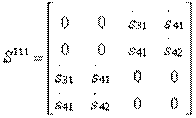
Условия и 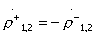, определяющие направленность типа III, в терминах классических матриц передачи парциальных четырехполюсников дают уравнения

,

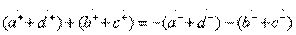
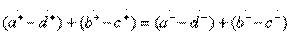из которых в силу вещественности элементов 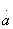и и 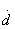мнимости элементов 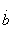и 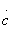в реактивном четырехполюснике следуют условия:

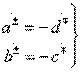направленность типа III,(3.42)

и с учетом этих условий получаем следующие выражения для элементов идеальной матрицы рассеяния (3.41):

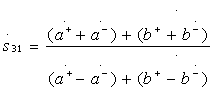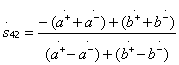; .(3.43)

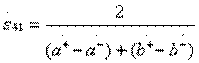
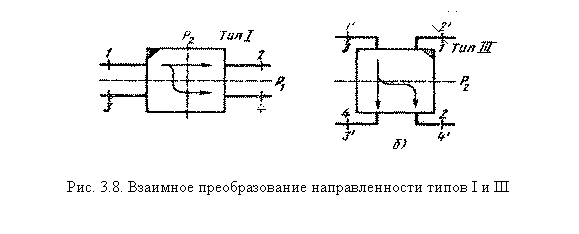
К направленным ответвителям типа III могут быть отнесены направленные ответвители типа 1, если они имеют вторую плоскость

геометрической симметрии 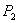(рис. 3.8, а). Действительно, поворот направленного ответвителя типа 1 в плоскости рисунка на 90° по часовой стрелке и перенумерация входов , , 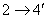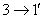и 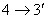приводят к ответвителю с матрицей рассеяния вида (3.41), т. е. к направленному ответвителю типа III, имеющему плоскость симметрии 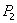. Поэтому в направленных ответвителях с двумя плоскостями геометрической симметрии настройка парциальных четырехполюсников симметричного и антисимметричного возбуждения по условиям (3.34) и (3.42) в ряде случаев может оказаться эквивалентной и привести к одинаковым схемам ответвителей (с точностью до перенумерации входов).

Пользуясь сформулированными условиями согласования и развязки входов направленных ответвителей в терминах параметров парциальных четырехполюсников, можно не только легко уяснить принцип действия того или иного ответвителя (разумеется, имеющего плоскость симметрии), но а получить соотношения, необходимые для его проектирования.