Анализ четырехполюсников каскадной структуры с помощью матриц передачи

Многие четырехполюсные и двухполюсные устройства СВЧ имеют каскадную структуру, характерную тем, что выход предшествующего четырехполюсника является входом последующего четырехполюсника и т. д. Анализ такого соединения значительно упрощается, если характеризовать четырехполюсники, а также и их объединение специальными матрицами - матрицами передачи. Особенностью матриц передачи является то, что в качестве воздействия на четырехполюсник используется пара электрических величин, определяющих режим одного входа (обычно второго), а в качестве реакции - соответствующая пара величин, определяющая режим другого входа (обычно первого).

При определении классической матрицы передачи (будем называть ее также матрицей А) связь воздействия и реакции имеет вид

(3.1)

или в алгебраической форме

(3.1, a)

Для определения физического смысла элементов матрицы А следует рассмотреть мысленные опыты холостого хода и короткого замыкания на входах четырехполюсника. Тогда следует:

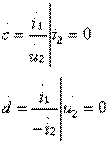(3.2)

Следовательно, элемент 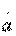— это коэффициент передачи по напряжению при размыкании выхода, элемент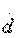 — коэффициент передачи по току при коротком замыкании на выходе. Элементы 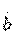и 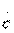соответственно представляют собой нормированные взаимное сопротивление при коротком замыкании и взаимную проводимость при холостом ходе на выходе.

Используя (3.1), легко показать, что классическая матрица передачи составного четырехполюсника на рис. 3.1 равна произведению матриц передачи парциальных четырехполюсников:

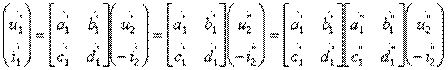
т. e. имеет место основное свойство матриц передачи:

А=А'А".(3.3)

Разумеется, это свойство матрицы передачи распространяется на любое число каскадно включенных четырехполюсников. Произведение двух матриц не подчиняется в общем случае переместительному закону, и поэтому перемножать матрицы передачи четырехполюсников при каскадировании нужно в той последовательности,. в которой они включены в тракт.

Наряду с классической матрицей передачи А при анализе каскадно включенных четырехполюсников СВЧ находит применение также и волновая матрица передачи Т, которая связывает между собой режимыпервого и второго входов в терминах падающих и отраженных волн:

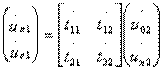(3.4)

Из-за смены порядка следования падающей и отраженной волн в столбце возбуждения, относящемся ко второму входу, волновая матрица передачи для каскадного соединения двух четырехполюсников определяется по правилу, аналогичному (3.3), т. е.

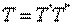.(3.5)

Таким образом, при использовании любых матриц передачи— классических или волновых—матрица каскадного соединения N различных четырехполюсников получается равной произведению N матриц передачи отдельных каскадов. Следует отметить, что элементы волновой матрицы передачи Т не имеют четкого физического смысла, за исключением элемента 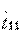, который равен обратной величине элемента 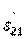матрицы рассеяния (т. е. ).

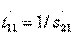Остановимся кратко на анализе двухполюсников каскадной структуры (рис. 3.2). Такие двухполюсники представляют собой каскадное соединение ряда четырехполюсников, последний из которых замыкается на оконечную нагрузку с сопротивлением 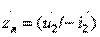. Входное сопротивление составного двухполюсника может быть найдено делением верхнего уравнения (3.1 а) на нижнее:

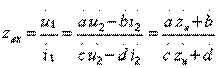(3.6)

Таким образом, анализ двухполюсника каскадной структуры сводится к нахождению матрицы передачи 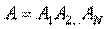с последующим использованием формулы (3.6).

Если оконечная нагрузка представляет собой короткое замыкание или холостой ход, то формула (3.6) упрощается и принимает одну из следующих форм:

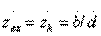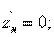
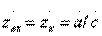при при 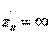(3.7)

Анализ каскадных двухполюсников может быть произведен' и в терминах матрицы передачи 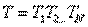. В этом случае деление второго уравнения (3.4) на первое с последующей подстановкой коэффициента отражения оконечной нагрузки позволяет найти входной коэффициент отражения составного двухполюсника:

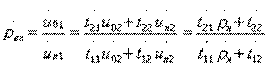(3.8)

Входной коэффициент отражения можно найти и по обычной формуле 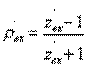подставляя в нее значение 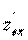из (3.6).