LU-разложение матрицы и основанный на нем метод решения системы
Пусть решается СЛАУ (5), при этом имеется LU-разложением матрицы системы. Тогда метод решения СЛАУ, основанный на LU-разложении заключается в следующем. Исходная система 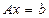 представляется в эквивалентном виде:
представляется в эквивалентном виде:
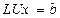 . (35)
. (35)
Обозначим произведение матрицы 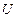 на вектор неизвестных
на вектор неизвестных 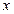 через вектор новых неизвестных
через вектор новых неизвестных 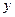 :
:
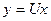 , (40)
, (40)
тогда система (35) примет вид:
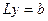 . (45)
. (45)
Таким образом, чтобы решить исходную систему (5) общего вида в методе, основанном на LU-разложении, надо решить последовательно две системы, но с треугольными матрицами: сначала СЛАУ (45), в результате получим вектор 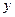 , а затем СЛАУ (40), подставив в правую часть уже известный
, а затем СЛАУ (40), подставив в правую часть уже известный 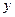 .
.
СЛАУ (45) – система с нижней треугольной матрицей с единицами на главной диагонали:
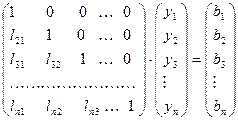 .
.
Ее решение происходит сверху вниз путем последовательной подстановки уже найденных значений 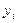 . После того, как
. После того, как 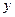 найден, решается СЛАУ (40):
найден, решается СЛАУ (40):
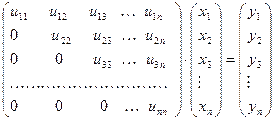 .
.
Решение производится снизу вверх путем выполнения последовательной подстановки уже найденных на предыдущих шагах значений 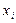 .
.
Таким образом, основные шаги метода решения СЛАУ (5), основанного на LU-разложении матрицы системы, следующие:
Шаг 1. Построить LU-разложение матрицы СЛАУ: 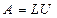 ;
;
Шаг 2. Решить СЛАУ 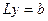 , в результате решения получить вектор
, в результате решения получить вектор 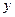 ;
;
Шаг 3. Решить СЛАУ 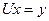 , в результате решения получить искомый вектор
, в результате решения получить искомый вектор 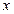 .
.
Дата добавления: 2015-08-21; просмотров: 1954;
