Алгоритм вычисления обратной матрицы методом присоединенной матрицы.
1. Находим определитель исходной матрицы. Если определитель равен нулю, то обратной матрицы не существует. Если определитель отличен от нуля, то матрица А невырожденная и обратная матрица существует.
2. Находим присоединенную матрицу А*, элементы которой являются алгебраическими дополнениями элементов транспонированной матрицы А. 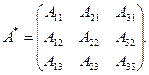
3. Вычислим обратную матрицу по формуле
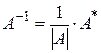 , где
, где 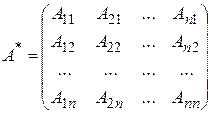 .
.
4. Проверяем правильность вычисления А-1×А = А×А-1 = Е. (Е – единичная матрица)
Матрицы А и А-1 взаимообратные. Если |A| = 0, то обратная матрица не существует.
Пример 1.Дана матрица А. Убедиться, что она невырожденная, и найти обратную матрицу 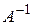 .
.
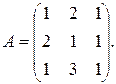
Решение: 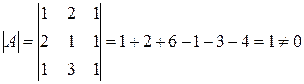 . Следовательно матрица невырожденная.
. Следовательно матрица невырожденная.
Найдем обратную матрицу. Составим алгебраические дополнения элементов матрицы А.
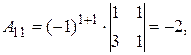
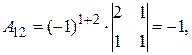
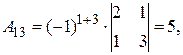
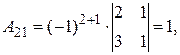
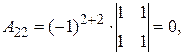
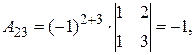
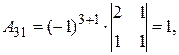
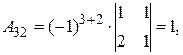
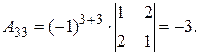
Получаем 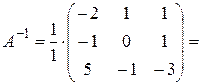
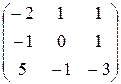 .
.
Дата добавления: 2015-08-21; просмотров: 2351;
