Свойства определителей
10. Величина определителя не изменится, если его строки и столбцы поменять местами.
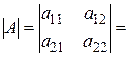
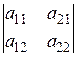 ,
, 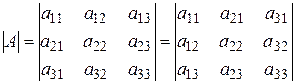
20. Перестановка двух строк или столбцов определителя равносильна умножению его на (-1).
30. Если определитель имеет две одинаковые строки или два одинаковых столбца, то он равен нулю.
40. Умножение всех элементов строки или столбца определителя на любое число l равносильно умножению определителя на это число l.
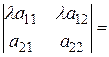
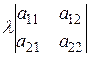 ,
, 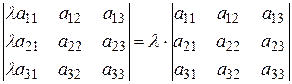
50. Если все элементы некоторого столбца или строки определителя равны нулю, то и сам определитель равен нулю.
60. Если элементы двух строк или двух столбцов определителя пропорциональны, то определитель равен нулю.
70. Если каждый элемент любого столбца или любой строки определителя представлен в виде двух слагаемых, то определитель можно представить в виде суммы двух определителей.
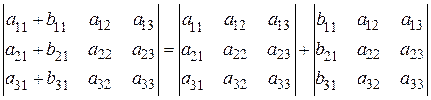 , аналогично для определителей 2-го порядка.
, аналогично для определителей 2-го порядка.
80. Если к элементам некоторой строки или столбца прибавить соответствующие элементы другой строки или столбца, умноженные на любой общий множитель l, то величина определителя не изменится.
Определение 3.Минором 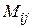 элемента
элемента 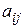 определителя называется определитель, полученный из данного определителя вычеркиванием строки и столбца, на пересечении которых расположен этот элемент, т.е. i – ой строки и j – го столбца.
определителя называется определитель, полученный из данного определителя вычеркиванием строки и столбца, на пересечении которых расположен этот элемент, т.е. i – ой строки и j – го столбца.
Определение 4.Алгебраическим дополнением 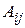 элемента
элемента 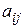 определителя называется минор этого элемента, умноженный на
определителя называется минор этого элемента, умноженный на 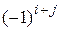 , т.е.
, т.е. 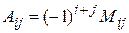 .
.
Для вычисления алгебраических дополнений элементов определителей третьего порядка знаки легко запомнить по следующей схеме: 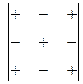 .
.
Например: 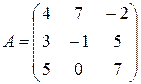
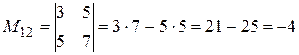 ;
;
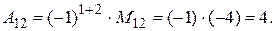
90. Определитель равен сумме произведений элементов какой-нибудь строки или столбца на их алгебраические дополнения.
Например: 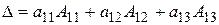 =
= 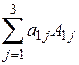 .
.
100. Сумма произведений элементов какого-нибудь столбца или строки определителя на алгебраические дополнения соответствующих элементов другого столбца или строки равна нулю.
Например: 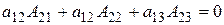 или
или 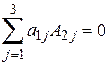 .
.
Лекция 3. Методы вычисления определителей n – го порядка. Разложение определителя матрицы по элементам строки и столбца.
Примеры вычисления определителей путём разложения по элементам строк или столбцов.
?????????????
1. Методы вычисления определителей n – го порядка.
Основываясь на понятиях определителей второго и третьего порядков, можно аналогично ввести понятие определителя порядка n. Определители порядка выше третьего вычисляются, как правило, с использованием свойств определителей, сформулированных в п. 1.3., которые справедливы для определителей любого порядка.
Используя свойство определителей номер 90 введем определение определителя 4-го порядка:
 .
.
Пример 2. Вычислить, используя подходящее разложение.
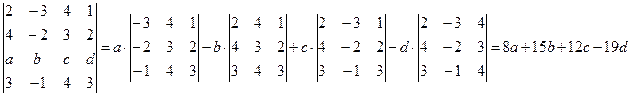 .
.
Аналогично вводится понятие определителя 5-го, 6-го и т.д. порядка. Значит определитель порядка n :
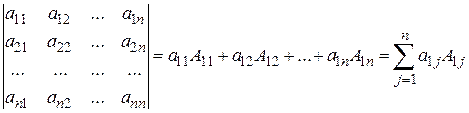 .
.
Все свойства определителей 2-го и 3-го порядков, рассмотренные раннее, справедливы и для определителей n-го порядка.
Рассмотрим основные методы вычисления определителей n-го порядка.
1. Метод понижения порядка определителя основан на следующем соотношении (i фиксированное число): 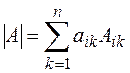 , где Аik алгебраические дополнения к
, где Аik алгебраические дополнения к 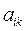 (разложение определителя по i-ой строке). Либо
(разложение определителя по i-ой строке). Либо 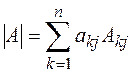 (разложение по j-тому столбцу).
(разложение по j-тому столбцу).
Замечание: прежде чем применять этот метод, полезно, используя основные свойства определителей, обратить в нуль все, кроме одного, элементы его некоторой строки или столбца. (Метод эффективного понижения порядка)
2. Метод приведения к треугольному виду заключается в таком преобразовании определителя, когда все его элементы, лежащие по одну сторону от главной диагонали, становятся равными нулю. В этом случае определитель равен произведению элементов его главной диагонали.
Пример 3. Вычислить, приведением к треугольному виду.
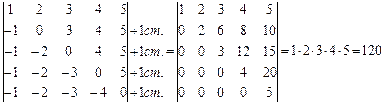
Пример 4.Вычислить, используя метод эффективного понижения порядка
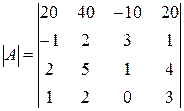 .
.
Решение: по свойству 40 определителей из первой строки вынесем множитель 10, а затем будем последовательно умножать вторую строку на 2, на 2, на 1 и складывать соответственно с первой, с третьей и четвертой строками (свойство 80).
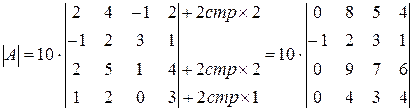 .
.
Полученный определитель можно разложить по элементам первого столбца. Он будет сведен к определителю третьего порядка, который вычисляется по правилу Саррюса (треугольника).
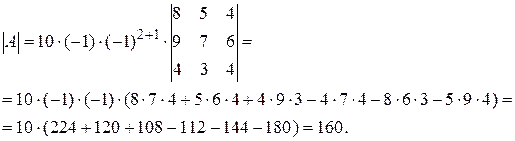
Пример 5.Вычислить определитель, приведением к треугольному виду.
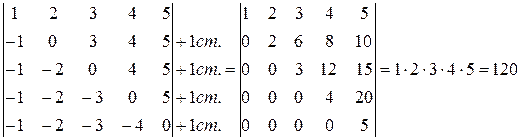 .
.
Пример 3. Вычислить, используя рекуррентные соотношения.
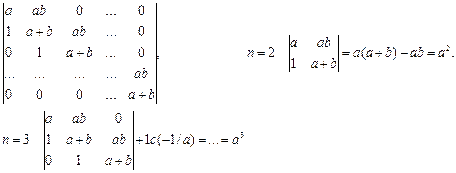
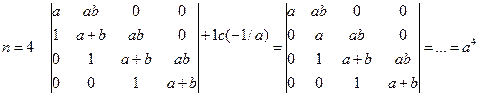 .
.
 .
.
Дата добавления: 2015-08-21; просмотров: 1958;
