Лекция 1. Матрицы. Действия с матрицами.
1.1 Понятие матрицы.
Определение 1. Матрицей А размера m ´ n называется прямоугольная таблица из m строк и n столбцов, состоящая из чисел или иных математических выражений 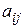 (называемых элементами матрицы), i = 1,2,3,…,m, j = 1,2,3,…,n.
(называемых элементами матрицы), i = 1,2,3,…,m, j = 1,2,3,…,n.
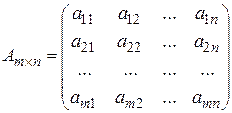 , или
, или 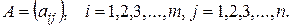
Определение 2. Две матрицы 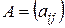 и
и 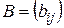 одного размера называются равными, если они совпадают поэлементно, т.е.
одного размера называются равными, если они совпадают поэлементно, т.е. 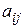 =
= 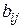 , i = 1,2,3,…,m, j = 1,2,3,…,n.
, i = 1,2,3,…,m, j = 1,2,3,…,n.
С помощью матриц легко записывать некоторые экономические зависимости, например таблицы распределения ресурсов по некоторым отраслям экономики.
Определение 3. Если число строк матрицы совпадает с числом ее столбцов, т.е. m = n, то матрица называется квадратной порядка n, а в противном случае прямоугольной.
Определение 4. Переход от матрицы А к матрице Ат , в которой строки и столбцы поменялись местами с сохранением порядка, называется транспонированиемматрицы.
Виды матриц: квадратная (размера 3´3) - 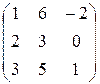 ,
,
прямоугольная (размера 2´5) - 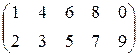 ,
,
диагональная - 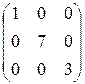 , единичная -
, единичная - 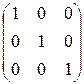 , нулевая -
, нулевая - 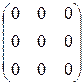 ,
,
матрица-строка - 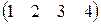 , матрица-столбец -
, матрица-столбец - 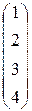 .
.
Определение 5.Элементы квадратной матрицы порядка n с одинаковыми индексами называются элементами главной диагонали, т.е. это элементы: 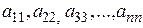 .
.
Определение 6.Элементы квадратной матрицы порядка n называются элементами побочной диагонали, если сумма их индексов равна n + 1, т.е. это элементы: 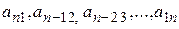 .
.
Дата добавления: 2015-08-21; просмотров: 1167;
