Операции над матрицами.
10. Суммой двух матриц 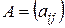 и
и 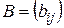 одинакового размера называется матрица С = (сij), элементы которой определяются равенством сij = aij + bij, (i = 1,2,3,…,m, j = 1,2,3,…,n).
одинакового размера называется матрица С = (сij), элементы которой определяются равенством сij = aij + bij, (i = 1,2,3,…,m, j = 1,2,3,…,n).
Свойства операции сложения матриц.
Для любых матриц А,В,С одного размера выполняются равенства:
1) А + В = В + А (коммутативность),
2) (А + В) + С = А + (В + С) = А + В + С ( ассоциативность).
20. Произведениемматрицы 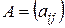 на число l называется матрица
на число l называется матрица 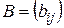 того же размера, что и матрица А, причем bij = l
того же размера, что и матрица А, причем bij = l 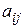 (i = 1,2,3,…,m, j = 1,2,3,…,n).
(i = 1,2,3,…,m, j = 1,2,3,…,n).
Свойства операции умножения матрицы на число.
1. l×(mА) = (l×m)А (ассоциативность умножения);
2. l(А+В) = lА+lВ (дистрибутивность умножения относительно сложения матриц);
3. (l+m)А = lА+mА (дистрибутивность умножения относительно сложения чисел).
Определение 7. Линейной комбинацией матриц 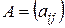 и
и 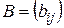 одинакового размера называется выражение вида a×А+b×В, где a и b - произвольные числа.
одинакового размера называется выражение вида a×А+b×В, где a и b - произвольные числа.
30. Произведением А×В матриц А и В соответственно размеров m´n и n´k называется матрица С размера m´k, такая, что элемент сij равен сумме произведений элементов i-той строки матрицы А и j-того столбца матрицы В, т.е. сij = ai1b1j+ai2b2j+…+aikbkj.
Произведение АВ существует, только в том случае, если число столбцов матрицы А совпадает с числом строк матрицы В.
Свойства операции умножения матриц:
1. (А×В)×С = А×(В×С) (ассоциативность);
2. (А+В)×С = А×С+В×С (дистрибутивность относительно сложения матриц);
3. А×(В+С) = А×В+А×С (дистрибутивность относительно сложения матриц);
4. А×В ¹ В×А ( не коммутативность).
Определение 8.Матрицы А и В, для которых АВ = ВА, называются коммутирующими или перестановочными.
Умножение квадратной матрицы любого порядка на соответствующую единичную матрицу не меняет матрицу.
Определение 9. Элементарными преобразованиями матриц называются следующие операции:
1. Перемена местами двух строк (столбцов).
2. Умножение каждого элемента строки (столбца) на число, отличное от нуля.
3. Прибавление к элементам одной строки (столбца) соответствующих элементов другой строки (столбца).
Определение 10.Матрица В, полученная из матрицы А с помощью элементарных преобразований называется эквивалентной (обозначается В~А).
Пример 1.1. Найти линейную комбинацию матриц 2А–3В, если
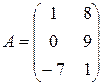 ,
, 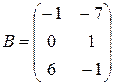 .
.
Решение:
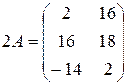 ,
, 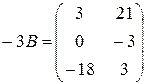 ,
,
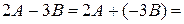
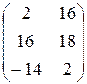
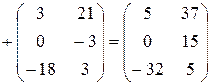 .
.
Пример 1.2. Найти произведение матриц 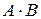 , если
, если
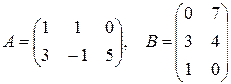 .
.
Решение: т.к количество столбцов первой матрицы совпадает с количеством строк второй матрицы, то произведение матриц существует. В результате получаем новую матрицу 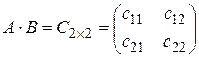 , где
, где
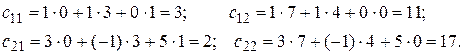
В результате получим 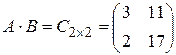 .
.
Дата добавления: 2015-08-21; просмотров: 1713;
