Арифметические операции с пределами.
Теорема 1: Пусть 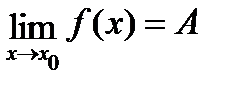 , а
, а 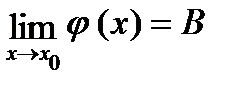 , тогда
, тогда 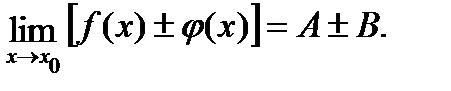
Док-во: По теореме о представлении функций, имеющих предел: f(x)=A+a(x), где a(x) – б/м при x®x0, а j (x)=B+b(x), где b(x) ‒ б/м при x®x0.
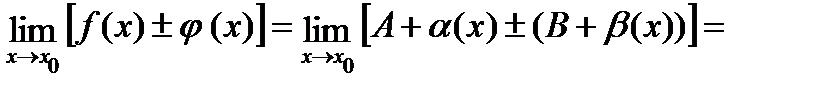
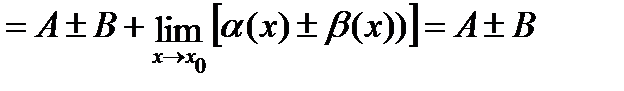
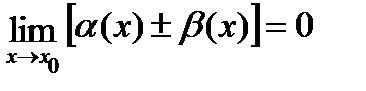 , как сумма двух б/м.
, как сумма двух б/м.
Ч.т.д.
Теорема 2: Пусть 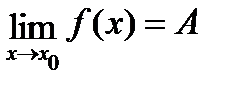 , а
, а 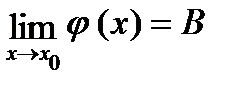 , тогда
, тогда 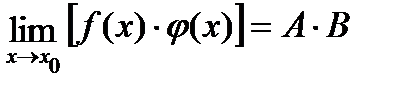 .
.
Док-во: По теореме о представлении функций, имеющих предел: f(x)=A+a(x), где a(x) – б/м при x®x0, а j (x)=B+b(x), где b(x) ‒ б/м при x®x0.
f(x)·j (x)= (A±a(x))·(B+b(x))=A·B+A·b(x)+ a(x)·B+ a(x)·b(x)=A·B, так как A·b(x) и a(x)·B и a(x)·b(x) стремятся к нулю при x®x0 по свойствам б/м. Переходя к пределу при x®x0 получаем требуемое.
Ч.т.д.
Теорема 3: Пусть 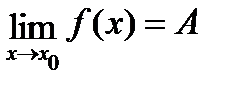 , а
, а 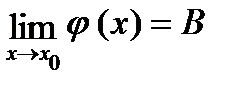 , тогда
, тогда 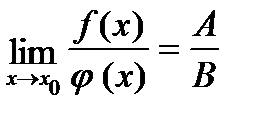 , где B¹0.
, где B¹0.
Доказывается теорема аналогично теоремам 1 и 2.
Следствие: 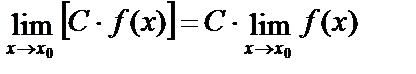 , где C-const.
, где C-const.
Неопределенности. Если не применимы основные теоремы о пределах, свойства б/м и б/б, то возникают неопределенности вида: 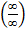 ,
, 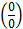 , (0·¥), (1¥), (00), (¥0), (¥-¥).
, (0·¥), (1¥), (00), (¥0), (¥-¥).
Рассмотрим три вида неопределенности: 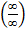 , (¥-¥),
, (¥-¥), 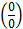 .
.
Пример. Вычислить пределы.
1) 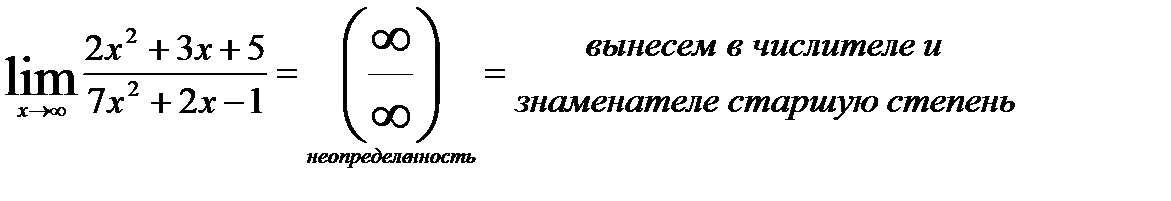 =
=  =
= 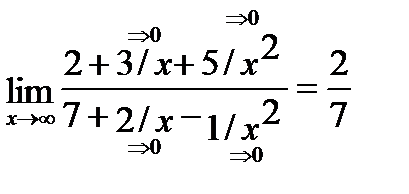
2) 
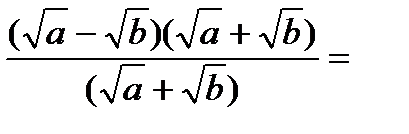
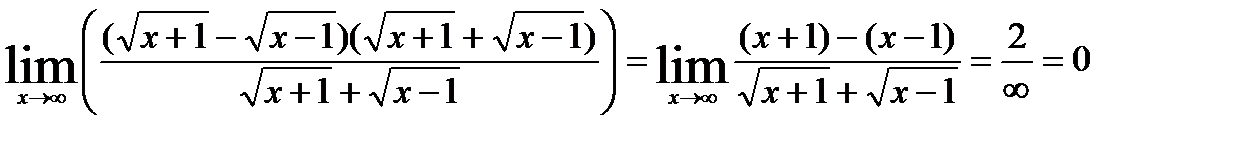
3) 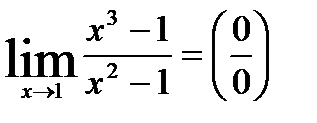
от неопределенности избавимся следующим образом: разложим числитель и знаменатель на множители и сократим.
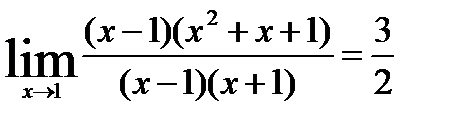
4) 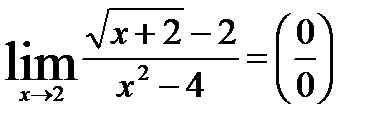
чтобы избавиться от иррациональности, надо умножить и поделить на сопряженное выражение.
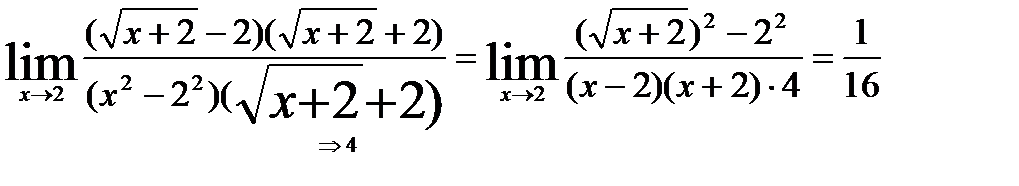
Дата добавления: 2015-08-11; просмотров: 2378;
