Необходимое и достаточное условие существования предела функции.

Теорема о представлении функции, имеющей предел:

Для того чтобы число Абыло пределомфункции f(x) при x®x₀ , необходимо и достаточно, чтобы в некоторой окрестности точки x₀ f(x) была представима следующим образом: f(x)=A+a(x), где a(x) – б/м при .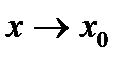

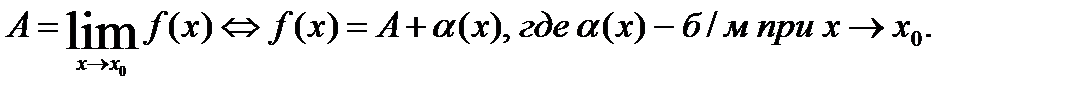
Док-во:

Необходимость. Пусть

Þ" 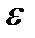>0 $ d>0: из |x-x₀| <d следует неравенство |f(x)-A| < .

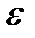Это неравенство означает, что f(x)–A=a(x) ‒ б/м при x®x₀ (по определению б/м). Отсюда f(x)=A + a(x).

Достаточность. В некоторой окрестности точки x₀ функция представима в виде: f(x) = A+a(x), где a(x) – б/м при x®x₀. Þ a(x)=f(x)–A – б/м, то есть по определению: " 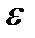>0 $ d>0 из неравенства |x-x₀| <d Þ|f(x) – A|< .

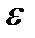Последнее неравенство означает, что .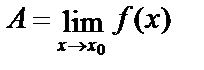

Ч.т.д.