Единственность предела функции.

Теорема: Если функция имеет предел при x®a, то он единственен.

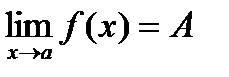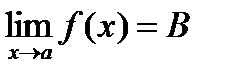Док-во: Предположим противное. Пусть у функции существуют два предела при x®a и . Возьмем e>0 так, чтобы окрестности точек A и B не пересекались. По определению предела функции: существует такое d>0, что из |x-a|<d следует |f(x)-A|<e, |f(x)-B|<e, т.е. значения f(x) лежат одновременно в e-окрестности точки A и e-окрестности точки B, чего быть не может, т.к. окрестности не пересекаются, полученное противоречие доказывает теорему.

Ч.т.д.