Свойства сходящихся последовательностей.

1. Единственность.

Теорема: Сходящаяся последовательность имеет только один предел.

2. Арифметические действия.

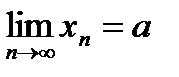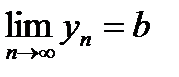Теорема: Если последовательности {x_n} и {y_n} сходящиеся, причем и , тогда 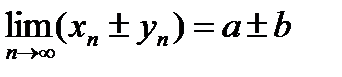; ; 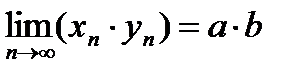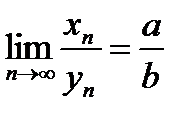при условии .

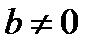3. Необходимое условие сходимости.

Теорема Больцано-Вейерштрасса:

Сходящаяся последовательность ограничена.

Док-во:

Пусть последовательность {х_n} сходится Þ существует конечный предел 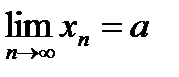Þ по определению: для "e > 0 $ номер N, начиная с которого .

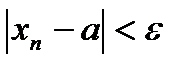Из неравенства: .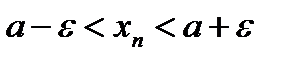

Выберем С=max { }.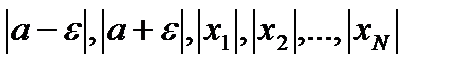

Значит, для членов последовательности {x_n} выполняется неравенство 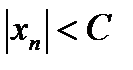. Тогда по определению последовательность {x_n} ограничена.

Ч.т.д.

4. Достаточные условия существования предела.

Определение: Последовательность {x_n} называется возрастающей (неубывающей), если x₁<x₂<… (x₁£x₂£…).

Пример: 1<2<3<4<…, {x_n} – возрастает.

1£1<2£2<3£3…, {x_n} - неубывающая.

Определение: Последовательность {x_n} называется убывающей (невозрастающей), если x₁>x₂>… (x₁³x₂³…).

Пример: 1>1/2>1/4>…, {x_n} – убывающая.

1³1/2³1/2>1/3³1/3>…, {x_n} - невозрастает.

Теорема1: Если последовательность монотонно возрастает и ограничена сверху, то она имеет конечный предел.

Теорема2: Если последовательность монотонно убывает и ограничена снизу, то она имеет конечный предел.

Док-во:

Докажем теорему 1.

{x_n} возрастет Þ x₁<x₂<….

{x_n} ограничена сверху Þ существует число М такое, что при "n x_n 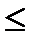М. Отступим от М на e, тогда существует номер N, начиная с которого

М-e< x_n 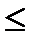М.

x_n

М

М-e

0 1 2 3 4 n

Усилим правую часть неравенства:

М-e< x_n<М+e, т.е. .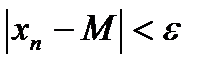

Значит, для "e > 0 $ номер N, начиная с которого справедливо

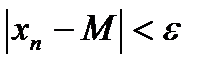. Þ . Þ по определению: {x_n} сходится.

Теорема 2 доказывается аналогично.

Ч.т.д.