Сходящиеся и ограниченные последовательности.

Определение: Последовательность называется сходящейся, если она имеет конечный предел.

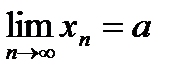- число.

В противном случае последовательность называется расходящейся.

Определение: Последовательность {x_n} называется ограниченной сверху, если существует число M такое, что для всех членов последовательности x_n 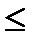M.

Определение: Последовательность {x_n} называется ограниченной снизу, если существует число m такое, что для всех членов x_n³m.

Определение: Последовательность называется ограниченной, если она ограниченна сверху и снизу, т.е. $ число A>0 такое, что для всех членов последовательности |x_n|£A.