Предел функции.
Пусть функция y=f(x) определена в некоторой окрестности точки a, за исключением, может быть самой точки.
1) Определение предела функции на языке 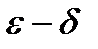 :
:
Число А называется пределом функции f(x) при x®a, если для любого сколь угодно малого положительного числа e найдется число d(e)>0 такое, что для всех x, отличных от a и удовлетворяющих неравенству |x-a|<d, следует неравенство |f(x)-A|<e.
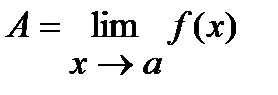 Þ "e>0 $d>0: из |x-a|<d Þ |f(x)-А|<e.
Þ "e>0 $d>0: из |x-a|<d Þ |f(x)-А|<e.
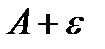
| y |
A
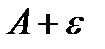
| х |
   |
Интервал (a-d, a+d) на оси ОХ называется дельта-окрестностью точки a.
Интервал (A-e, A+e) на оси ОY называется эпсилон-окрестностью точки A.
Функция y=f(x) переводит каждую точку из d-окрестности точки a на оси ОХ внутрь ε-окресности точки А на оси ОY.
2) Определение предела на языке окрестности:
Число A называется пределом функции при x®a, если для любой сколь угодно малой e-окрестности точки A на оси ОY найдется d-окрестность точки a на оси ОХ, которую функция переводит в e-окрестность.
3) Определение предела на языке последовательности:
Число A называется пределом функции f(x) при x®a, если для любой последовательности {xn}, сходящейся к точке a, соответствующая последовательность значений функции {f(xn)} сходится к A.
4) Правый и левый пределы.
Определение: Если есть xn®a и xn<a, то число A называется левым пределом функции при x®a-0.
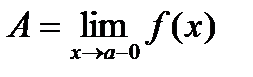 .
.
Определение: Если xn®a и xn>a, то число A называют правым пределом функции при x®a+0.
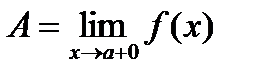 .
.
Такие пределы называются односторонние.
Замечание 1: Для существования предела функции не требуется, чтобы функция была определена в самой точке x=a, достаточно того, что она определена в ее окрестности.
Замечание 2: На последовательность {xn} можно смотреть как на функцию натурального аргумента xn=f(n), nÎN. Поэтому все свойства пределов и теоремы для пределов функции справедливы и для предела последовательности.
Дата добавления: 2015-08-11; просмотров: 896;
