Теоремы о предельном переходе в неравенствах.
Теорема 1. Теорема о «двух милиционерах».
Пусть заданы 3 функции f(x), j(x), g(x) такие, что f(x)£j(x)£g(x). Тогда если
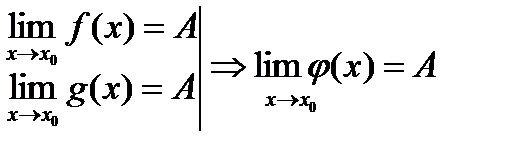
Док-во: Вычтем А из всех частей неравенства f(x)£j(x)£g(x):
f(x)-A£j(x)-A£g(x)-A.
По теореме о представлении функции, имеющей предел: f(x)=A+a(x), g(x)=A+b(x), где a(x) и b(x) являются б/м. Между двумя б/м может находиться только б/м Þ по теореме о представлении функции, имеющей предел: 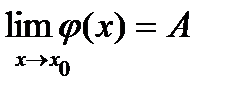 .
.
Ч.т.д.
Теорема 2: Пусть функция f(x)³0 и существует конечный предел 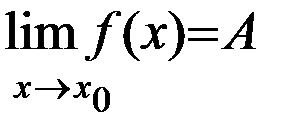 . Тогда A³0.
. Тогда A³0.
Док-во: Предположим противное: A<0. Тогда окрестность точки A лежит по оси ОY ниже начала координат. Þ В этой окрестности f(x)<0, чего быть не может.
Ч.т.д.
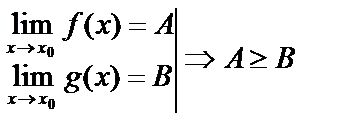 Теорема 3: Если f(x)³g(x) и
Теорема 3: Если f(x)³g(x) и
Док-во: Из неравенства f(x)³g(x) Þ f(x)-g(x)³0. По предыдущей теореме и арифметическим операциям 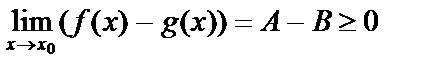 Þ A³B.
Þ A³B.
Ч.т.д.
Дата добавления: 2015-08-11; просмотров: 1393;
