Глава 3. Теоремы о дифференцируемых функциях.

Для дифференцируемых функций выполняется ряд важных для приложений теорем. Перечислим основные теоремы.

Теорема Вейерштрасса.

Если функция непрерывна на замкнутом промежутке [a, b], то она достигает на этом промежутке наибольшего M и наименьшего m значений.

При этом могут возникать три случая.

1. Наименьшее и наибольшее значения достигаются внутра промежутка [a, b] (рис.3.1а).

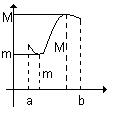
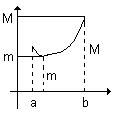
а б в

Рис. 3.1. Наибольшее и наименьшее значение функции на интервале.

2. На границе достигается либо только наибольшее, либо только наименьшее значение (рис. 3.1б).

3. На границе достигается и наибольшее и наименьшее значение (рис. 3.1в).