Сравнение бесконечно малых.

Рассмотрим отношение двух б/м a(x) и b(x), т.е. a(x) и b(x) ®0 при x®x₀.

Определение: Если 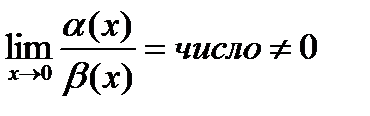, тогда б/м a(x) и b(x) называются б/м одного порядка малости.

Определение: Если 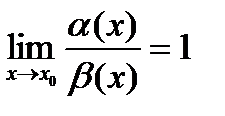, тогда б/м a(x) и b(x) называются эквивалентными.

Обозначаются: a(x)~ b(x).

Определение: Если 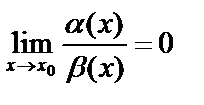, тогда б/м a(x) имеет порядок малости выше, чем б/м b(x).

Определение: Если 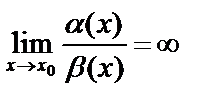, тогда б/м b(x) имеет порядок малости выше, чем б/м a(x).

Теорема: Если при x®x₀ б/м a(x)~ a*(x), а б/м b(x)~ b*(x), то ; .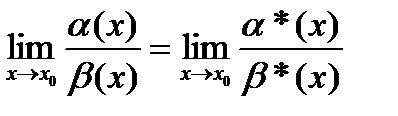

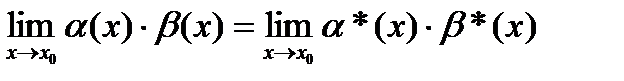Тогда при x®x₀ и a(x) ‒ б/м справедливо:

sina(x)~ a(x); e^a(x)-1~a(x); ln(1+a(x))~ a(x); a^a(x)-1~a(x)·lna;

tga(x)~ a(x); arcsina(x)~ a(x); arctga(x)~ a(x); (1+a(x))^a-1~a·a(x).