Интеграл по значению Коши. Сравнение сходимости интеграла по значению Коши и несобственного интеграла

План

1. Сведение несобственного интеграла ІІ рода к несобственному интегралу І рода

Интеграл по значению Коши. Сравнение сходимости интеграла по значению Коши и несобственного интеграла

1. Сведение несобственного интеграла ІІ рода к несобственному интегралу І рода

Пусть 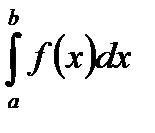- НИ ІІ рода, 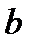- особая точка подинтегральной функции. Сделаем замену при вычислении НИ ІІ рода: 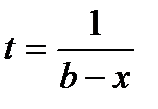. В результате получим:

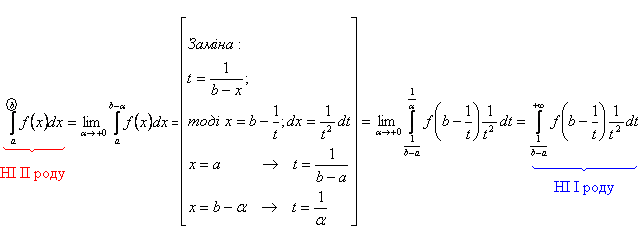
Таким образом, существование 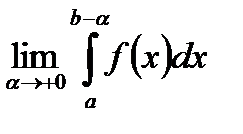равносильно существованию 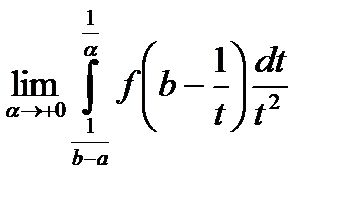, а поэтому сходимость (расходимость) НИ ІІ рода 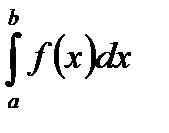равносильна сходимости (расходимости) НИ І рода 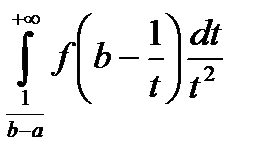. Если один из них сходится, то

.

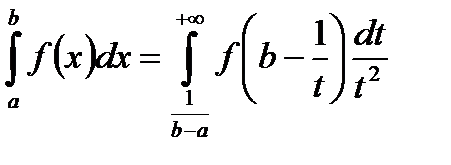Интеграл по значению Коши. Сравнение сходимости интеграла по значению Коши и несобственного интеграла

Пусть функция 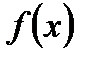определена на 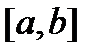. Допустим, что для 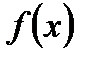т. 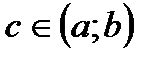- особая. Тогда, в соответствии с лекцией 39, имеем:

.

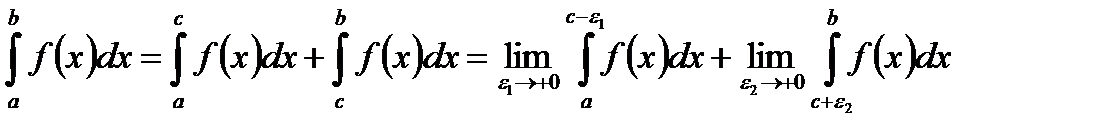Если не существует хотя бы один из этих пределов, то НИ ІІ рода 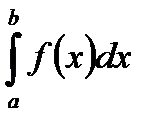является расходящимся. Тут 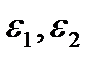- независимые друг от друга.

Коши предложил вариант, когда :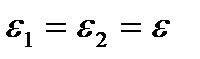

.

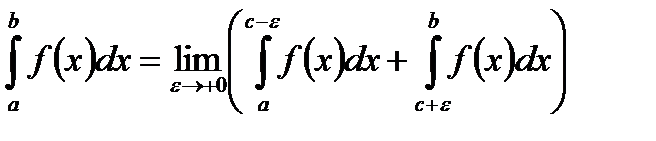При таком вычислении 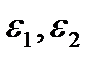уже не являются независимыми – они равны. Такой способ вычисления не является общим. Возможны такие случаи, когда пределы 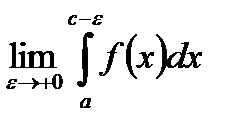, 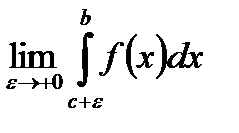отдельно не существуют, но существует предел суммы 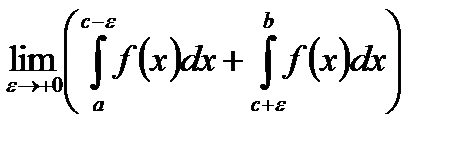. Тогда такой предел называется главным значением по Коши несобственного интеграла (или интегралом по значению Коши) и обозначается

.

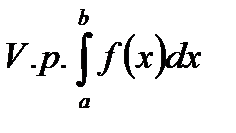Пусть 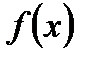определена на 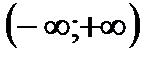, а НИ І рода

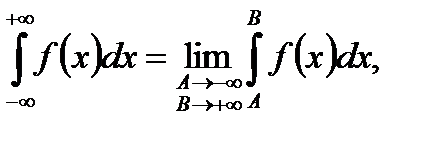
где 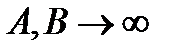независимо друг от друга, расходится. Но может случиться, что если взять симметричный промежуток, т.е. 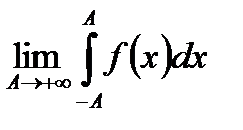, то он будет существовать. Тогда этот предел называется НИ І рода за Коши и обозначается:

.

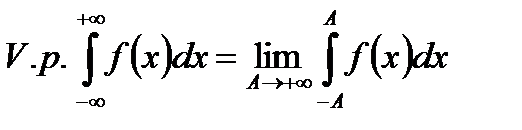Пример. Рассмотрим НИ І рода 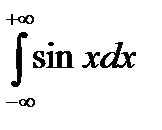. В классическом определении НИ І рода он является расходящимся, поскольку:

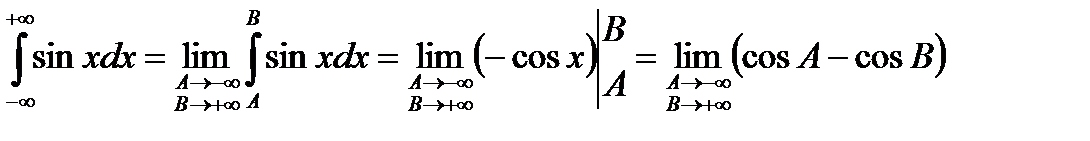не существует.

Но

.

.

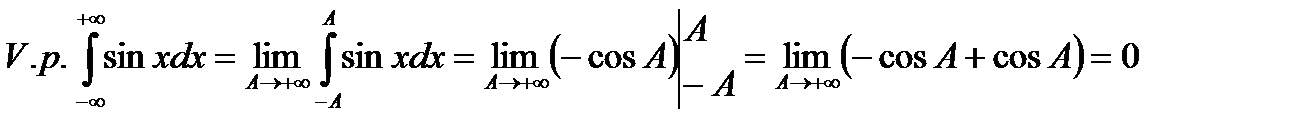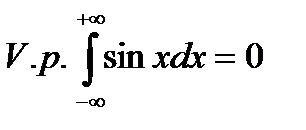Целесообразность такого вычисления для рассмотренного примера становится очевидной из рис.1.

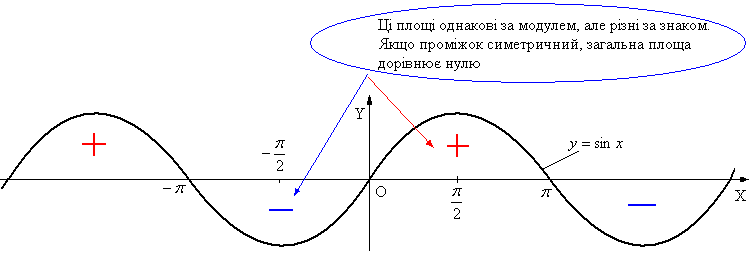
Рис.1.

Пример. Рассмотрим 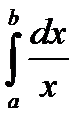, где 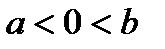. Этот НИ ІІ рода, как было установлено в предыдущей лекции, расходится. Вычислим его значение по Коши:

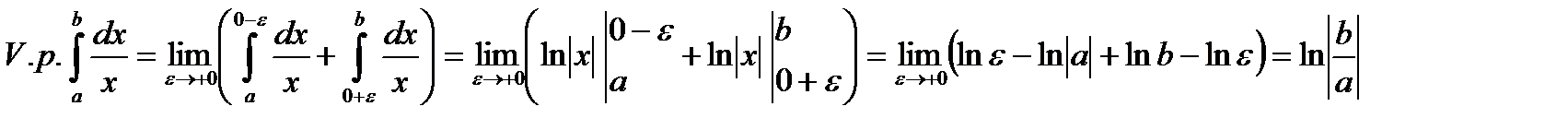
Таким образом, по Коши интеграл 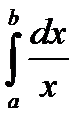является сходящимся.

Пример. Интеграл 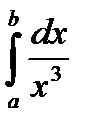, где 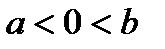, является расходящимся в классическом смысле. Но

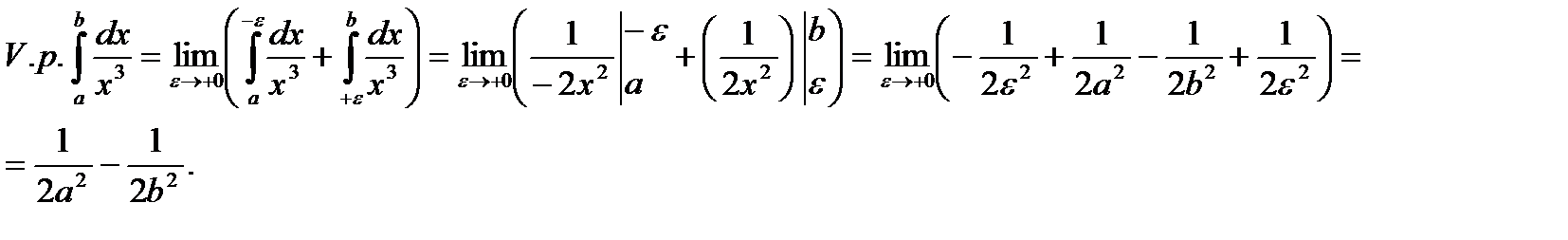
Утверждение 1. Если функция 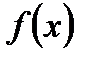определена на 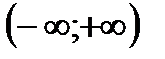и является нечетной, то

,

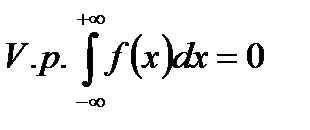а если 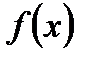- четная, то

.

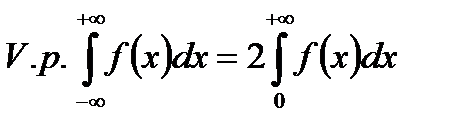Доказательство. Пусть 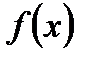определена на 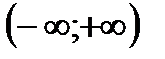и является нечетной. Тогда:

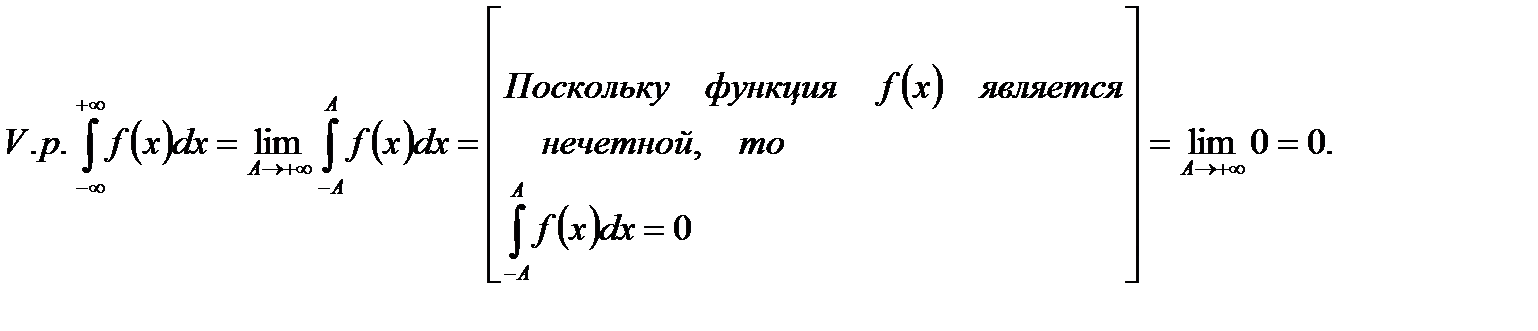
Аналогично для четной функции.

Вопросы

1. Можно ли НИ ІІ рода свести к НИ І рода? Как именно?

2. Что такое интеграл по значению Коши?

3. В чем заключается смысл определения НИ по Коши?

4. Как определяется интеграл по Коши для четной функции?

5. Как определяется интеграл по Коши для нечетной функции?