Вторая пара уравнений Максвелла в интегральной форме
13.2.1. Первое уравнение второй пары - это теорема о циркуляции + что-то еще.
Для вектора 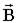 теорема о циркуляции (11.5.4) гласит:
теорема о циркуляции (11.5.4) гласит:
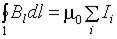 . .
| (11.5.4) |
В вакууме:
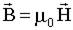 .
.
Тогда
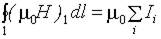 , ,
| или | 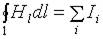 . .
|
При непрерывном распределении тока через поверхность S
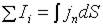 ,
,
здесь j - плотность тока (10.2).
Тогда имеем
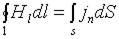 .
.
Интеграл слева берется по произвольному воображаемому контуру, интеграл справа - по произвольной поверхности, "натянутой" на этот контур.
В веществе теорема о циркуляции для вектора 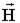 имеет тот же вид:
имеет тот же вид:
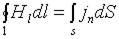 ,
,
но при этом в интеграле справа не учитываются микроскопические токи вещества, приводящие к изменению магнитной индукции в веществе (12).
13.2.1.1. + что-то еще - это "ток смещения"
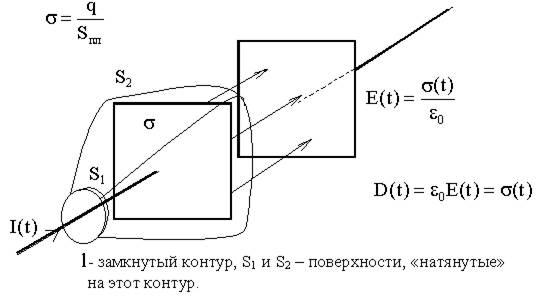
Применим теорему о циркуляции вектора 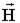 к магнитному полю, созданному переменным электрическим током, перезаряжающим конденсатор.
к магнитному полю, созданному переменным электрическим током, перезаряжающим конденсатор.
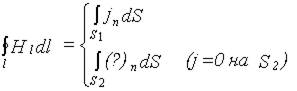 ,
,
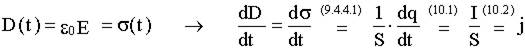 .
.
См. (9.4.4.1) , (10.1), (10.2).
На S2 j = 0, но 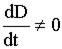 , а по величине
, а по величине 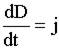 , значит ?
, значит ? 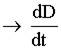 .
.
Величину 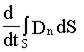 Максвелл назвал "током смещения".
Максвелл назвал "током смещения".
Как видно, "ток смещения" - это переменное во времени электрическое поле.
Первое уравнение второй пары утверждает, что магнитное поле создается током проводимости и переменным электрическим полем ("током смещения").
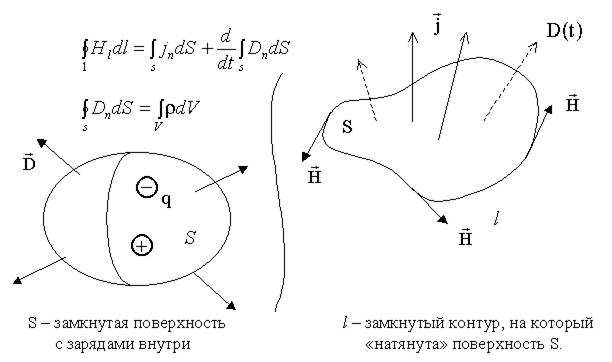
13.2.2. Второе уравнение второй пары - это теорема Гаусса для вектора  (9.13.4)
(9.13.4)
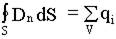 ,
,
где qi - свободные, не связанные заряды.
При непрерывном распределении заряда
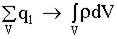 .
.
Дата добавления: 2015-08-08; просмотров: 983;
