Система уравнений Максвелла в дифференциальной форме

Применяя теорему Стокса можно преобразовать интеграл по замкнутому контуру l в интеграл по поверхности S, натянутой на этот контур.

Теорема Остроградского-Гаусса позволяет преобразовать интеграл по замкнутой поверхности S в интеграл по объему, ограниченному этой поверхностью. Преобразовав левые части уравнений (13.3) можно получить систему Максвелла в дифференциальной форме:

Первая пара:

,

.

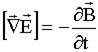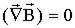Вторая пара:

,

.

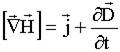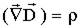Здесь

.

К этим уравнениям необходимо добавить закон Ома в дифференциальной форме и связь с , с :

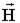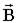см. (10.5),

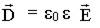
см. (9.13.4),

см. (12.5).

Эти три векторных уравнения характеризуют свойства среды. Семь записанных выше уравнений составляют основу электродинамики покоящихся сред.

Литература,

1. Савельев И.В. Курс общей физики. - М.: Наука. 1982. - т.1

2. Савельев И.В. Курс общей физики. - М.: Наука. 1982. - т.2

3. Савельев И.В. Курс физики. - М.: Наука. 1989 . - т.1

4. Савельев И.В. Курс физики. - М.: Наука. 1989 . - т.2

5. Трофимова Т.И. Курс физики. - M.: Высшая школа. 1990

6. Киттель Ч., Найт У., Рудерман М. Механика. - М. Физматлит. 1971

7. Парсел Э. Электричество и магнетизм. - М.: Физматлит. 1973

8. Принцип относительности. Сборник работ по специальной теории относительности./ Составитель - Тяпкин А.А. М.: Атомиздат. 1973

9. Физический энциклопедический словарь./ Гл. редактор Прохоров А.М.. М.: Советская энциклопедия. 1973

10. Кудрявцев П.С. Курс истории физики. - М.: Просвещение, 1982