Таким чином, розповсюдження збудження (хвилі) зі швидкістю вздовж напрямку зобразиться функцією, в аргумент якої параметри та входять у вигляді комбінації або .

Така будова аргумента показує, що значення функції 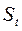, яке вона має в точці 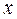в момент часу 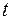, повториться в більш віддаленій точці 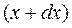в більш пізнішій момент часу 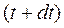, якому відповідає функція .

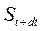Якщо ці значення дійсно однакові, тобто 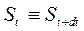то повинні бути рівні аргументи функції :

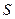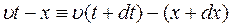(1)

Таким чином збудження за час 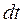переміститься на відстань 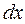, розповсюджуючись зі швидкістю .

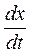Із співвідношення (1) видно, що :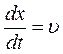

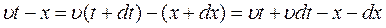
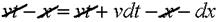
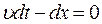
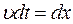
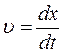
Таким чином: будь-яка функція, яка залежить від аргумента 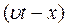відображає розповсюдження збудження вздовж 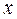в напрямку зростаючих значень 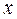з постійною швидкістю .

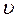Аналогічно, будь-яка функція від аргумента 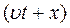описує розповсюдження хвилі зі швидкістю 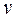в бік спадаючих значень .

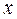Встановимо вид рівняння, що описує розглянутий хвильовий процес.

· по-перше, рівняння хвильового процесу має диференційну форму;

· по-друге містить значення .

Можна показати, що рівняння, рішенням якого буде функція від аргумента 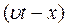або 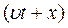, має вид:

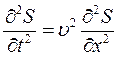
Рішенням такого рівняння буде співвідношення:

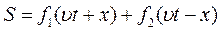
Дане рішення є сукупністю двох хвиль, що розповсюджуються зі швидкістю v у протилежних напрямках від точки виникнення збурення.

Швидкість хвилі. Хвиля - це поширення коливань у просторі. Тому можна говорити про швидкість v цього розповсюдження. Ця швидкість називається швидкістю хвилі. Ми тільки що бачили , що за час , що дорівнює періоду Т , коливання поширюється на відстань, рівну довжині хвилі. значить, λ = ʋ Т.

Оскільки період коливань пов᾿язаний з частотою коливань співвідношенням Т = 1 / ν, то λ = ʋ / ν, звідки

ʋ = λ ν