Второе уравнение Максвелла в интегральной форма. Ток смещения

Основная идея теории Максвелла заключается во взаимосвязи электрических и магнитных полей: если переменное магнитное поле порождает в окружающем пространстве электрическое поле, то, в свою очередь, и переменное электрическое поле должно создавать в окружающем пространстве магнитное поле.

Следовательно, в теореме о циркуляции вектора 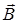к источникам магнитного поля в виде токов проводимости добавляется еще один источник, который Максвелл назвал током смещения:

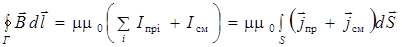. (10.11)

Формула (10.11) получила название закона полного тока. Под током смещения I_см понимают скалярную физическую величину, измеряемую в амперах, характеризующую способность электрического поля создавать магнитное поле и пропорциональную скорости изменения во времени напряженности 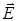электрического поля.

Установим формулу связи плотности тока смещения 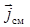с напряженностью 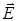переменного электрического поля. Для этого рассмотрим электрическую цепь, содержащую плоский конденсатор с площадью пластин S(рис.10.6а). Протекание переменного тока в такой цепи сопровождается плавным переходом на границе пластин конденсатора тока проводимости в ток смещения, который существует в пространстве внутри конденсатора. Записывая условие непрерывности не границе обкладок, получим

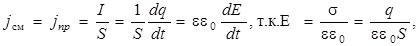
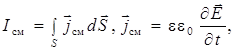(10.12)

где σ – поверхностная плотность заряда на пластинах конденсатора; 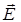- напряженность электрического поля внутри конденсатора; ε – относительная диэлектрическая проницаемость среды между обкладками.

Подставляя формулу (10.12) в выражение (10.11), получим второе уравнение Максвелла в интегральной форме следующего вида:

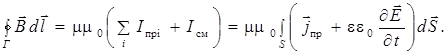(10.13)

Уравнение (10.13) читается следующим образом: циркуляция вектора 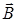магнитного поля по произвольному замкнутому контуру Гравна сумме токов проводимости и смещения, охватываемых контуром Г, умноженной на коэффициент (μμ₀).

Физический смысл уравнения (10.13) заключается в том, что источниками магнитного поля являются токи проводимости, микротоки и переменное электрическое поле.