В результате последнее уравнение принимает вид

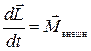, (1.5.11)

Где — суммарный момент всех внешних сил.

Уравнение (1.5.11) утверждает: производная момента импуль­са системы по времени равна суммарному моменту всех внешних сил. Разумеется, оба момента здесь определены относительно одной и той же точки O заданной системы отсчета.

Итак, мы пришли к важному выводу: согласно уравнению (1.5.11), момент импульса системы может изменяться под действием только суммарного момента всех внешних сил. Отсюда непосредственно вытекает и другой важный вывод — закон сохранения момента импульса: момент импульса замкнутой системы частиц остается постоянным, т. е. не меняется со временем, причем это справедливо для момента импульса, взятого относительно любой точки инерциальной системы отсчета.

При этом моменты импульса отдельных частей или частиц замкнутой системы могут изменяться со временем. Однако эти изменения всегда происходят так, что приращение момента импульса одной части системы равно убыли момента импульса ее другой части (конечно, относительно одной и той же точки системы отсчета).

Закон сохранения момента импульса играет такую же важную роль, как и законы сохранения энергии и импульса. Уже сам по себе он позволяет сделать во многих случаях ряд существенных заключений о свойствах тех или иных процессов, со­вершенно не вникая в их детальное рассмотрение.

Особый интерес представляют случаи, когда момент импульса сохраняется для незамкнутых систем. Если относительно не­которой точки O выбранной системы отсчета суммарный момент внешних сил равен нулю в течение интересующего нас промежутка времени, то, согласно (1.5.11), момент импульса сис­темы относительно точки O сохраняется за это время. В незамкнутых системах такой точки, вообще говоря, может и не быть, что следует, прежде всего, выяснить для каждого конкретного случая.

В более ограниченном случае у незамкнутых систем может сохраняться не сам момент импульса, а его проекция на некоторую неподвижную ось Z. Это бывает тогда, когда проекция суммарного момента всех внешних сил на эту ось Z равна нулю. В самом деле, записав уравнение (9.12) в проекциях на ось Z, получим

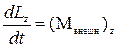. (1.5.12)