Закон сохранения момента импульса

Выберем произвольную систему частиц. Введем понятие мо­мента импульса данной системы как векторную сумму момен­тов импульсов ее отдельных частиц:

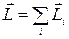, (1.5.10)

Где все векторы определены относительно одной и той же точки O заданной системы отсчета. Заметим, что момент импульса системы — величина аддитивная: момент импульса системы равен сумме моментов импульсов ее отдельных частей незави­симо от того, взаимодействуют они между собой или нет.

Выясним, какая величина определяет изменение момента импульса системы. Продифференцируем (1.5.10) по времени. Производная момента импульса i –ой частицы равна моменту всех сил, действующих на i-ую частицу. Представим этот момент в виде суммы моментов внутренних и внешних сил. Тогда

.