Здесь и — момент импульса и суммарный момент внешних сил относительно оси Z.

Из уравнения (1.5.12) следует, что если относительно некоторой неподвижной в данной системе отсчета оси Z проекция момента внешних сил равна нулю, то момент импульса системы относительно этой оси сохраняется:

(1.5.13)

При этом вектор 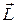, определенный относительно произвольной точки O на этой оси, может меняться. Например, если система движется в однородном поле тяжести, то суммарный мо­мент всех сил тяжести относительно любой неподвижной точки O перпендикулярен вертикали, а значит, относительно любой вертикальной оси момент силы тяжести равен нулю и _z = const, чего нельзя сказать о векторе .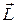

Рассуждения, которые приводят к закону сохранения мо­мента импульса, целиком опираются на справедливость законов Ньютона. А как обстоит дело в системах, не подчиняющихся этим законам, например в системах с электромагнитным из­лучением, в атомах, ядрах и др.?

Учитывая громадную роль, которую играет закон сохранения момента импульса, в физике понятие момента импульса расширяют на немеханические системы (которые не подчиняются законам Ньютона) и постулируют закон сохранения мо­мента импульса для всех физических процессов.

Такой расширенный закон сохранения момента импульса уже не является следствием законов Ньютона, а представляет собой самостоятельный общий принцип, являющийся обобщением опытных фактов. Наряду с законами сохранения энергии и импульса закон сохранения момента импульса является одним из фундаментальных законов природы.