Сложение гармонических колебаний одного направления и одинаковой частоты
 Пусть тело одновременно участвует в двух гармонических колебаниях одинаковой частоты, происходящих в одном направлении, причем амплитуды и начальные фазы колебаний различны (А1 ≠ А2, φ01 ≠ φ02):
Пусть тело одновременно участвует в двух гармонических колебаниях одинаковой частоты, происходящих в одном направлении, причем амплитуды и начальные фазы колебаний различны (А1 ≠ А2, φ01 ≠ φ02):
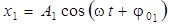 ,
, 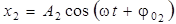 .
.
Результирующее движение, равное сумме колебаний х1 и х2, будет гармоническим колебанием той же циклической частоты ω:
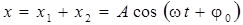 . (11.10)
. (11.10)
|
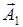 и
и 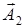 под углами φ01 и φ02 к оси Ох и приведем их во вращение с угловой скоростью ω (рис. 11.3).
под углами φ01 и φ02 к оси Ох и приведем их во вращение с угловой скоростью ω (рис. 11.3).
Оба вектора вращаются против часовой стрелки с одинаковой угловой скоростью ω, поэтому угол φ2 – φ1 между ними все время остается неизменным. Проекции векторов 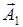 и
и 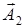 на ось Ох совершают гармонические колебания. Результирующее колебание будет изображаться проекцией на ось Ох вектора
на ось Ох совершают гармонические колебания. Результирующее колебание будет изображаться проекцией на ось Ох вектора  , полученного из векторов
, полученного из векторов 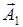 и
и 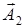 по
по
правилу параллелограмма. Из построения на рис. 11.3 следует, что (по теореме косинусов)
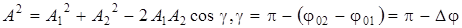 ,
,
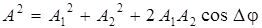 . (11.11)
. (11.11)
Из треугольников ∆ОА1В и ∆ОАС для начальной фазы φ0 результирующего колебания следует выражение
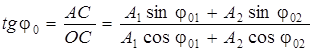 . (11.12)
. (11.12)
Рассмотрим частные случаи сложения колебаний.
1а. 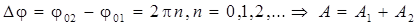 ,
,
то есть, если разность фаз складываемых колебаний равна четному числу π, то тогда колебания максимально усиливают друг друга.
1б. 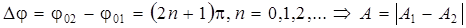 ,
,
то есть, если разность фаз складываемых колебаний равна нечетному числу π, то тогда колебания максимально ослабляют друг друга.
2. Биения –это колебания, которые возникают в результате сложения двух гармонических колебаний х1 и х2 одного направления с близкими частотами (ω2, ω1 >> ∆ω = ω2 – ω1):
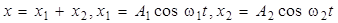 .
.
Рассмотрим подробнее результаты сложения таких колебаний. Для простоты будем считать, что амплитуды складываемых колебаний одинаковы: А1 = А2 = А. Используя известную формулу сложения косинусов, получим:
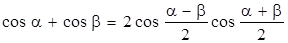
и определим:
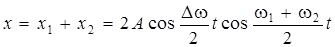 . (11.13)
. (11.13)
Первый сомножитель в выражении (11.13) изменяется со временем значительно медленнее второго (∆ω << ω1, ω2), поэтому можно считать, что результирующее колебание представляет собой колебание с циклической частотой ω = (ω1 + ω2)/2 и с изменяющейся со временем амплитудой биений:
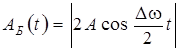 . (11.14)
. (11.14)
Итак, биения можно представить как колебания с периодически изменяющейся амплитудой; эти колебания не являются гармоническими. При этом период изменения амплитуды (период биений ТБ) и циклическая частота биений Ω будут определяться по формулам:
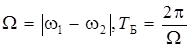 . (11.15)
. (11.15)
На рис. 11.4 приведены графики изменения амплитуды биения АБ и смещения х м. т. от времени. Метод биений применяют, например, для настройки музыкальных инструментов.
|

Дата добавления: 2015-08-08; просмотров: 1512;
