Затухающие колебания. Затухающие колебания наблюдаются в замкнутой механической системе (Fвнеш = 0), в которой имеются потери энергии на преодоление сил сопротивления

Затухающие колебания наблюдаются в замкнутой механической системе (F_внеш = 0), в которой имеются потери энергии на преодоление сил сопротивления, или в закрытом колебательном контуре (U_внеш = 0), в котором наличие сопротивления R приводит к потере энергии колебаний из-за нагревания проводников. В первом приближении можно считать, что при небольших скоростях движения, силы, вызывающие затухание механических колебаний, пропорциональны величине скорости. Будем называть эти силы, независимо от их происхождения, силами трения,или сопротивления:

,

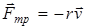где r– коэффициент сопротивления. Знак минус указывает, что сила трения всегда направлена в сторону, противоположную направлению движения.

Запишем второй закон Ньютона для затухающих колебаний тела вдоль оси ОХ:

ma_x = - kx- rv_x .

Заменив 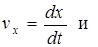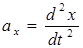и перенеся все члены в левую часть уравнения, получим

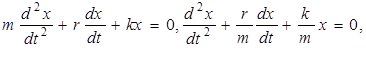
(12.1)

где 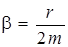- коэффициент затухания.

Если β ≤ ω₀, то в результате решения дифференциального уравнения (12.1) получается следующая зависимость смещения от времени:

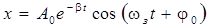, (12.2)

где е – основание натуральных логарифмов.

Выражение

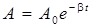(12.3)

называют амплитудой затухающих колебаний.

Величину

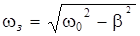(12.4)

называют собственной циклической частотой затухающих колебаний.

Затухающие колебания представляют собой непериодические колебания, так как в них никогда не повторяются, например, максимальные значения смещения, скорости и ускорения. Поэтому называть ω_з циклической частотой можно лишь условно. По этой же причине

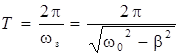, (12.5)

обычно называемую периодом затухающих колебаний, правильнее называть условным периодом затухающих колебаний.

Отношение амплитуд для моментов времени, отличающихся на период, равно

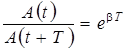. (12.6)

Это отношение называют декрементом затухания, а его логарифм – логарифмическим декрементом затухания:

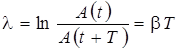. (12.7)

На рис.12.1 дан график функции (12.2).