Гармонические колебания. К колебательным движениям относят такие движения, которые характеризуются той или иной степенью повторяемости во времени описывающих их величин
К колебательным движениям относят такие движения, которые характеризуются той или иной степенью повторяемости во времени описывающих их величин. С колебаниями мы встречаемся при изучении самых различных физических явлений: звука, света, переменного тока, радиоволн и т. д.
 Не смотря на большое разнообразие колебательных процессов, как по физической природе, так и по степени сложности, все они совершаются по некоторым общим закономерностям и могут быть сведены к совокупности простейших периодических колебаний, называемых гармоническими.
Не смотря на большое разнообразие колебательных процессов, как по физической природе, так и по степени сложности, все они совершаются по некоторым общим закономерностям и могут быть сведены к совокупности простейших периодических колебаний, называемых гармоническими.
К периодическим колебаниям относят колебания, при которых описывающие их величины повторяются через промежуток времени, называемый периодом Т. При гармонических колебаниях (ГК) эти величины изменяются по гармоническому закону, то есть по закону синуса или косинуса.
|
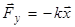 , где к – коэффициент упругости а
, где к – коэффициент упругости а 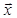 - вектор смещения шара из положения равновесия.
- вектор смещения шара из положения равновесия.
По мере приближения шара к положению равновесия числовое значение упругой силы уменьшается и в точке Остановиться равной нулю. За счет приобретенной кинетической энергии шар будет продолжать свое движение, растягивая пружину. Когда вся кинетическая энергия превратится в потенциальнуюэнергию, шар на мгновение остановится, после чего упругая сила растянутой пружины заставит его возвращаться в положение равновесия и т. д.
Колебания, которые возникают в системе, не подверженной действию переменных внешних сил, в результате какого-либо начального отклонения этой системы от состояния устойчивого равновесия, называют свободными. Если система консервативная, то при колебаниях не происходит рассеяния энергии. В этом случае свободные колебания называют незатухающими.
Покажем, что незатухающие колебания пружинного маятника будут гармоническими. Согласно второму закону Ньютона
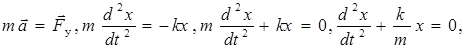 или
или
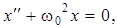 (11.1)
(11.1)
где 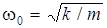 .
.
Уравнение (11.1) является дифференциальным уравнением колебаний. Из теории дифференциальных уравнений следует, что решением приведенного уравнения являются гармонические колебания
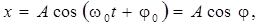 (11.2)
(11.2)
то есть смещение тела от положения равновесия изменяется по гармоническому закону. В уравнение (11.2) введены такие понятия, как:
А – максимальное смещение, или амплитуда колебания;
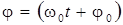 – фаза колебания, выражение стоящая под знаком синуса или косинуса;
– фаза колебания, выражение стоящая под знаком синуса или косинуса;
φ0 – начальная фаза колебаний – фаза в начальный момент времени t= 0;
ω0 – циклическая (круговая) частота свободных незатухающих гармонических колебаний системы.
Циклическая частота ω0 связана с периодом колебаний и линейной частотой nсоотношениями
ω0 = 2π/Т= 2πn. (11.3)
Запишем выражения для проекций скорости, проекции ускорения на ось Ох, а так же для потенциальной, кинетической и полной энергии тела:
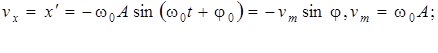 (11.4)
(11.4) 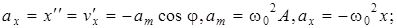 (11.5)
(11.5)
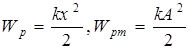 ; (11.6)
; (11.6)
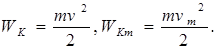 (11.7)
(11.7)
Покажем, что амплитуды колебаний кинетической и потенциальной энергии совпадают:
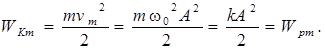 (11.8)
(11.8)
Тогда
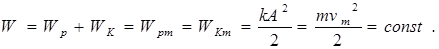 (11.9)
(11.9)
Из полученных формул следует, что проекция скорости vx и ускорения ах, кинетическая и потенциальная энергии тела изменяются по гармоническому закону подобно ее смещению х, а полная энергия колебаний остается при этом неизменной.
Приведем в пределах одного периода колебаний Тграфики зависимости х, vx, ах,WK, Wp и Wот времени t(рис.11.2, φ0 = 0).

|
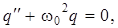
его решением является гармоническое колебание
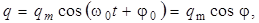
где q– заряд на обкладке конденсатора, 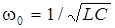 , L– индуктивность катушки, С – емкость конденсатора.
, L– индуктивность катушки, С – емкость конденсатора.
Дата добавления: 2015-08-08; просмотров: 810;
