Непрерывность функции.

Пусть функция y=f(x) определена в точке x₀ и некоторой ее окрестности.

Определение 1: Функция y=f(x) называется непрерывной в точке x₀, если она определена в этой точке и .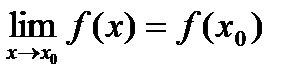

Dx=x-x₀ – приращение аргумента, Dy=f(x)-f(x₀)=f(x₀+Dx)-f(x₀) – приращение функции.

Определение 2: Функция y=f(x) называется непрерывной в точке x₀, если б/м приращению аргумента соответствует б/м приращение функции, т.е. .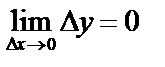

Определение 3: Функция y=f(x) называется непрерывной в точке x₀, если она определена в этой точке, оба односторонних предела существуют, конечны, равны между собой и равны значению функции в этой точке, т.е. .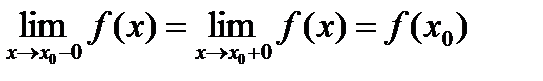

Определение: Функция y=f(x) называется непрерывной на промежутке, если она непрерывна в каждой точке этого промежутка.