Теоремы о непрерывных функциях.
Теорема 1. (о сохранении знака непрерывной функции).
Пусть функция f(x) определена и непрерывна на (а;b) и в точке х0 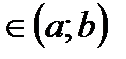 значение функции f(x0)
значение функции f(x0) 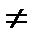 0. Тогда существует окрестность точки x0, в которой f(x) сохраняет знак.
0. Тогда существует окрестность точки x0, в которой f(x) сохраняет знак.
Теорема 2. (I т. Больцано-Коши).
| y |
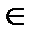 [а;b], что f(с)=0.
[а;b], что f(с)=0.
| x |
| f(a) |
| f(b) |
| b |
| c |
| a |
Замечание 1: Если выполняются условия этой теоремы, то график непрерывной функции обязательно пересечен осью ох.
Замечание 2: Если отказаться от условия непрерывности, то теорема не выполняется.
Теорема 3. (II т. Больцано-Коши о промежуточных значениях).
Пусть функция f(x) определена и непрерывна на [а;b], f(a)=А, f(b)=В. Тогда f(x) принимает все промежуточные значения между А и В.
Лемма о вложенных отрезках:
Дана последовательность вложенных отрезков, длины которых стремятся к нулю, т.е.:
[a1;b1] 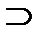 [a2;b2]
[a2;b2] 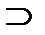 [a3;b3]
[a3;b3] 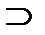 …
… 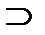 [an;bn]
[an;bn] 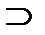 … .
… .
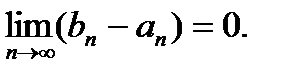 Тогда существует единственная точка, принадлежащая всем отрезкам.
Тогда существует единственная точка, принадлежащая всем отрезкам.
a1 a2 a3 . . . an… bn . . . b3 b2 b1
Рассмотрим последовательность левых концов:
{an} возрастает и ограничена сверху числом b1.
По теореме о пределе монотонной и ограниченной последовательности существует 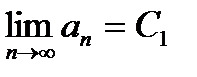 .
.
Рассмотрим последовательность правых концов:
{bn} убывает и ограничена снизу числом an 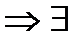
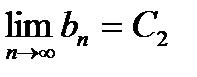
Рассмотрим С1 – С2= 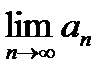 -
- 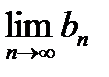 =
= 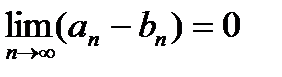
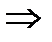 С1 = С2
С1 = С2  Существует единственная точкка, принадлежащая всем отрезкам.
Существует единственная точкка, принадлежащая всем отрезкам.
Теорема 4. (I т. Вейерштрасса).
Пусть функция f(x) непрерывна на [а;b]. Тогда f(x) ограничена на [а;b].
Док-во:
Предположим противное: функция f(x) не ограничена на [а;b]. Разделим [а;b] пополам и выберем ту часть, на которой f(x) не ограничена. Разделим эту часть пополам и выберем половину, на которой функция не ограничена и т.д.
Получим последовательность вложенных отрезков, длины которых стремятся к нулю.
Тогда по лемме о вложенных отрезках существует единственная точка С, принадлежащая всем отрезкам, такая, что в окрестности точки С функция f(x) не ограничена.
По условию теоремы f(x) непрерывна на [а;b]  f(x) непрерывна в точке С.
f(x) непрерывна в точке С.
По первому определению непрерывности  .
.
По определению предела: 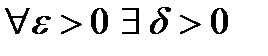 такое, что из неравенства
такое, что из неравенства 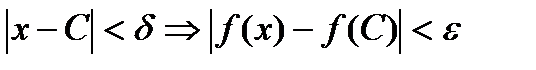
Положим 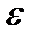 =1
=1 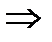
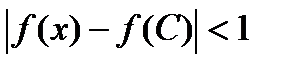 .
.
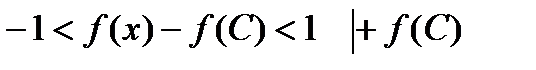
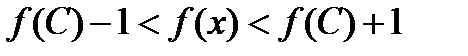
Выберем М=max( 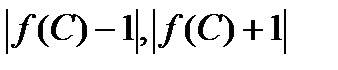 )
) 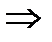
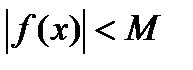
 f(x) ограничена в окрестности точки С.
f(x) ограничена в окрестности точки С.
Ч.т.д.
Теорема 5. (II т. Вейерштрасса).
Пусть функция f(x) непрерывна на отрезке [а;b]. Тогда она принимает на этом отрезке свое наибольшее и наименьшее значения.
| x |
| y |
| fнаиб |
| b |
| a |
| fнаим |
Дата добавления: 2015-08-11; просмотров: 801;
