Связь между непрерывностью функции и существованием производной.
Теорема: Если функция имеет конечную производную в точке x0, то она непрерывна в этой точке.
Док-во:
По определению производной: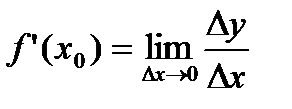 
= 
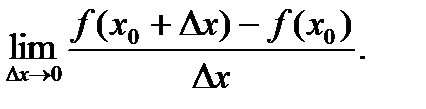
Обозначим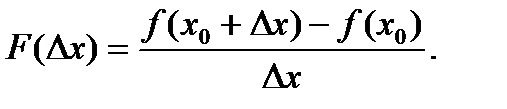 
Тогда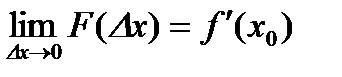 
.
По теореме о представлении функции, имеющей предел:
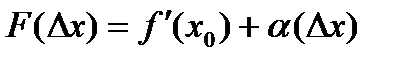, где 
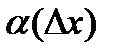‒ б/м при 
.
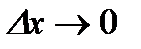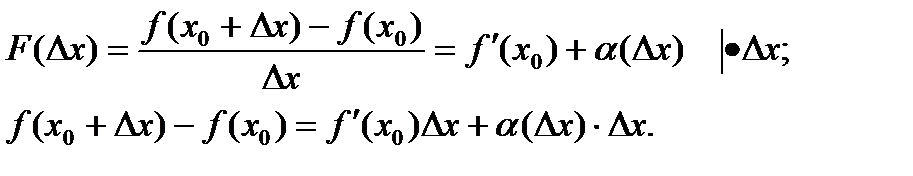
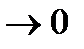
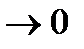
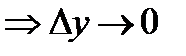при Δx→0.
По второму определению непрерывности, если б/м приращению аргумента соответствует б/м приращение функции, то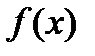 
непрерывна в точке х0.
Ч.т.д.
Дата добавления: 2015-08-11; просмотров: 4477;