Производная функции одной переменной.
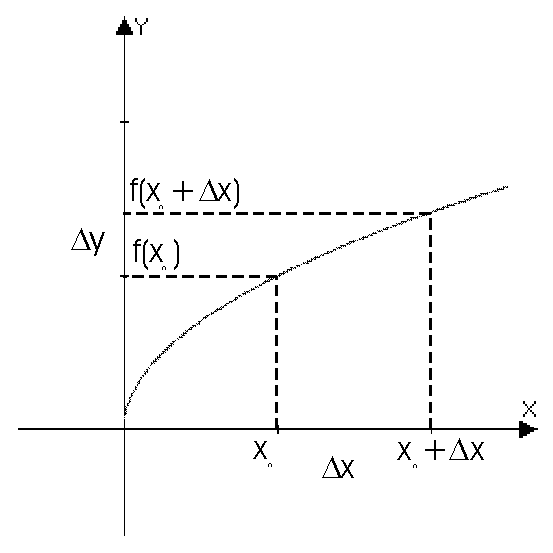 Определение: Пусть функция y=f(x) определена в точке x0 и некоторой ее окрестности. Дадим x0 приращение Dx так, чтобы точка
Определение: Пусть функция y=f(x) определена в точке x0 и некоторой ее окрестности. Дадим x0 приращение Dx так, чтобы точка 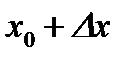 принадлежала указанной окрестности. Тогда функция получит приращение Dy.
принадлежала указанной окрестности. Тогда функция получит приращение Dy. 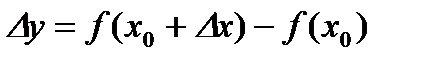 .
.
Если существует предел отношения приращения функции к приращению аргумента, когда последний стремится к нулю, то он называется производной функции f(x) в точке x0.
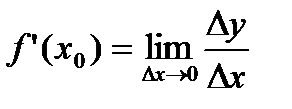 .
.
Обозначают производную 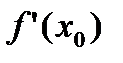 ,
, 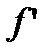 , y',
, y', 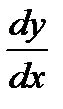 ,
, 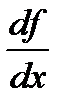 .
.
Замечание: Если изменить x0, то будет изменяться и производная функции в точке x0, следовательно, производная функции тоже является функцией.
Пример: Найти по определению производную функции y=x2.
Возьмем произвольную точку x, дадим приращение Dx, x®x+Dx. Функция получит приращение Dy: 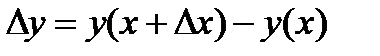 =
= 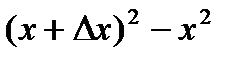 =
= 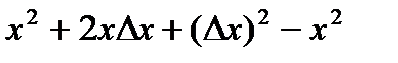 =
= 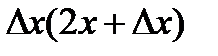 .
.
Рассмотрим предел 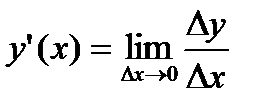 =
=  =
= 
Итак, производная 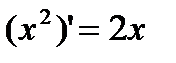 .
.
Дата добавления: 2015-08-11; просмотров: 752;
