Геометрический смысл производной.
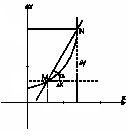На графике функции 
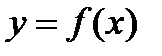возьмем точку М0 с координатами (x0,y0) и точку N с координатами ( 
; 
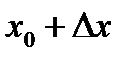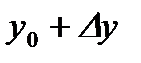). Проведем через эти точки секущую.
| x0 |
x0+  x
|
| y(x0+Dx) |
| y0=y(x0) |
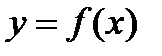в точке M0(x0,y0) называется предельное положение секущей M0N, когда точка N стремится к точке M0 по графику.
С одной стороны tga является угловым коэффициентом секущей, с другой стороны из прямоугольного треугольника: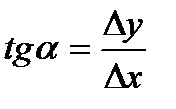 
.
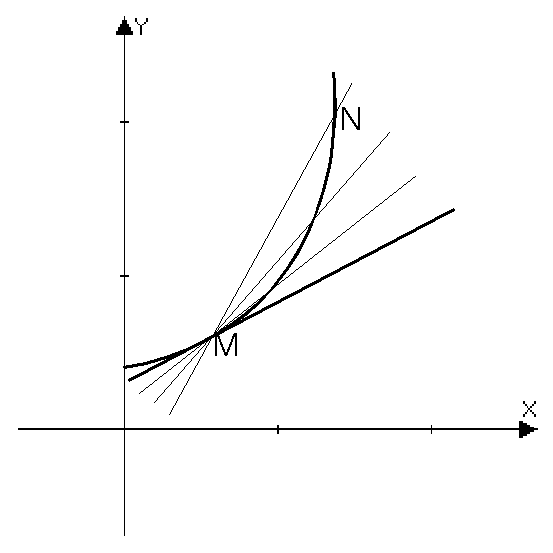Когда точка N®M по графику, тогда приращение
аргумента Dx®0, при этом угловой коэффициент
касательной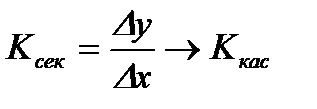 
.
Переходя к пределу при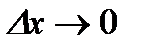 
,
получаем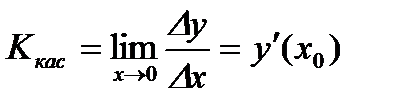 
.
Геометрический смысл производной заключается в следующем: производная функции в точке x0 равна угловому коэффициенту касательной, проведенной к графику функции в точке с абсциссой x0.
.
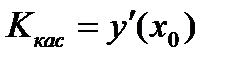Физический смысл производной.
Пусть материальная точка движется прямолинейно по закону S=S(t), где t ‒ время, S — координата точки на оси.
Физический смысл производной заключается в следующем: Производная – это мгновенная скорость изменения функции.
Vмгн=S'(t).
Дата добавления: 2015-08-11; просмотров: 751;