Вероятностный смысл волны де Бройля.

Волновая функция

Какова физическая природа волн де Бройля? Ответить на этот вопрос трудно, так как волны де Бройля имеют специфическую квантовую природу, не имеющую аналогии в классической физике.

Рис. 9.1

И все же между светом и движущимися частицами существует нечто общее. Этим общим является проявление волновых свойств через статистические закономерности. Рассмотрим явление дифракции света от щели (рис. 9.1). Если через щель проходит свет, то на экране наблюдается дифракционная картина. Используя волновые свойства, мы можем рассчитать, как будет меняться интенсивность света на экране с изменением координаты х.

Если рассматривать свет как поток частиц (фотонов), то для фотона мы не можем определить, в какую точку на экране он попадет. Для фотона можно рассчитать только вероятность попадания его в ту или иную точку (w). И эта вероятность w ~ I ~ A². Чтобы реализовать эту вероятность попадания фотонов в ту или иную точку на экране, необходимо пропустить большое число фотонов через щель. То есть получается, что волновые свойства света проявляются через статистические закономерности.

К такому же выводу мы придем, если в рассматриваемом эксперименте будем использовать поток частиц (волн де Бройля).

Чтобы описать распределение вероятности нахождения частиц в пространстве в квантовой механике используют волновую функцию ψ(х,у,z,t) (пси функцию). Пси функцию определяют следующим образом:

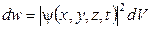dw– вероятность того, что частица находится в некотором элементарном объеме dV,пропорциональна .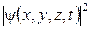

Физический смысл имеет не ψ-функция, а ее квадрат модуля, который определяет вероятность обнаружения частицы в данном объеме (точка):

<27 28 293031 32 33 >

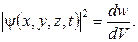
Дата добавления: 2015-08-08; просмотров: 1466;