Прохождение частиц через потенциальный барьер
|
Совершенно иначе выглядит поведение частицы согласно квантовой механике. В квантовой механике с помощью уравнения Шредингера определяется коэффициент прозрачности потенциального барьера D, который равен отношению интенсивности волны, прошедшей потенциальный барьер, к интенсивности волны, падающей на барьер. Для рассматриваемой задачи находят следующее выражение:
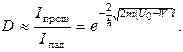(10.1)
|
В первом случае вероятность проникновения частицы через барьер большая, во втором – ничтожно мала.
Соответствующий расчет дает, что в случае потенциального барьера произвольной формы (рис. 10.2) формула (10.1) должна быть заменена более общей формулой:
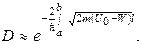
При преодолении потенциального барьера частица как бы проходит через «туннель» в этом барьере, в связи с чем рассмотренное нами явление называют туннельным эффектом.
С классической точки зрения туннельный эффект представляется абсурдным, так как частица, находящаяся в туннеле, должна обладать отрицательной кинетической энергией. Однако туннельный эффект – явление квантовое, не имеющее аналога в классической физике. В квантовой механике деление полной энергии на кинетическую и потенциальную не имеет смысла, так как противоречит принципу неопределенности. Действительно, тот факт, что частица обладает определенной кинетической энергией, был бы равнозначен тому, что частица имеет определенный импульс. Аналогично, тот факт, что частица имеет определенную потенциальную энергию U, означал бы, что частица находится в точно заданном месте пространства. А координата и импульс не могут одновременно иметь определенных значений. Таким образом, хотя полная энергия частицы Wимеет вполне определенные значения, она не может быть представлена в виде суммы точно определенных энергий Wки U. Ясно, что в этом случае заключение об отрицательности кинетической энергии внутри туннеля становится беспочвенным.
Дата добавления: 2015-08-08; просмотров: 832;