Орбитальный момент импульса и магнитный момент электрона в классической и квантовой механике

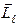Представим себе, что электрон в атоме движется со скоростью v по орбите радиуса r (рис. 10.3). Как любая движущая частица, электрон обладает моментом импульса ,который равен произведению момента инерции на угловую скорость:

.

Вектор 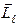перпендикулярен плоскости, в которой лежит орбита электрона, а его модуль

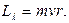
Движущийся по орбите электрон создает электрический ток, сила которого

,где 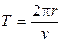-период обращения электрона вокруг ядра.

Электрический ток, текущий в замкнутом контуре, характеризуется магнитным моментом 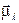.Направление вектора 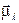связано с направлением тока правилом правого винта (рис. 10.3). Модуль магнитного момента равен произведению силы тока на площадь контура S:

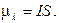Так какS=πr², получаем .

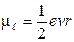Отношение магнитного момента 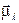частицы к ее механическому моменту 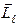,т. е.к ее моменту импульса, называют гиромагнитным отношением. Для электрона на орбите это отношение равно

.

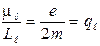Так как векторы 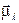и 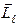антипараллельны, справедливо равенство

.

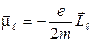В квантовой механике (из-за наличия волновых свойств) модуль орбитального момента импульса принимает дискретные значения. Используя уравнение Щредингера можно показать, что

,

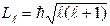где l– орбитальное квантовое число, которое может принимать следующие значения:

l = 0, 1, 2, … , n – 1.

Проекция этой физической величины на направление поля в пространстве определяется формулой:

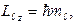
где магнитное квантовое число m_lпринимает значения:

m_l = 0, ±1, ±2 … , ± l.

Равенство и 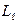запрещено соотношениями неопределенностей. Действительно, если бы выполнилось равенство отмеченных величин, произведение неопределенностей координаты и импульса в направлении поля (оси z) было бы равно 0.

В квантовой механике определенные значения имеют и 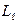.Проекции 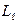на другие направления остаются неопределенными. Учитывая сказанное, вектор орбитального момента импульса 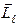можно представить как вектор, который равномерно вращается вокруг оси z, образуя с этой осью угол θ(рис. 10.4а), определяемый соотношением

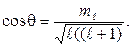
При заданном значении l m_lможет принимать (2l+ 1) значение.

Например, при l= 1, ,а L_lz=0, ± 1 (рис. 10.4б).

Магнитный момент электрона, обусловленный орбитальным движением, 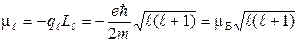,а его проекция на направление поля 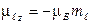,где 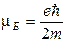-магнетон Бора.