Атом водорода в квантовой механике
На основании своих исследований Резерфорд в 1911 г. предложил ядерную (планетарную)модель атома. Согласно этой модели вокруг положительного ядра по замкнутым орбитам движутся электроны, образуя электронную оболочку атома, в области с линейными размерами порядка 10-10 м. Заряд ядра равен Zе (Z. -— порядковый номер элемента в системе Менделеева, е — .элементарный заряд), размер 10-15 – 10-14 м, масса, практически равна массе атома. Так как атомы нейтральны, то заряд ядра равен суммарному заряду электронов, т. е. вокруг ядра должно вращаться Z электронов.
Атом водорода и водородоподобные системы – это системы, состоящие из ядра с зарядом Ze и одного электрона (например, ионы He+, Li2+).
Решение задачи об энергетических уровнях электрона для атома водорода (а также водородоподобных систем: иона гелия Не+, двукратно ионизованного лития Li+ + и др.) сводится к задаче о движении электрона в кулоновском поле ядра.
Потенциальная энергия взаимодействия электрона с ядром, обладающим зарядом Zе (для атома водорода Z =1),
 , (1)
, (1)
где r – расстояние между электроном и ядром. Графически функция U (r)изображена жирной кривой на рис. 6, неограниченно убывающей (возрастающей .по модулю) при уменьшении r, т. е. при приближении электрона к ядру.
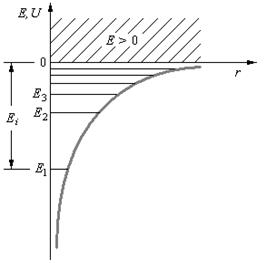
Рис. 6
Состояние электрона в атоме водорода описывается волновой функцией Ψ, удовлетворяющей стационарному уравнению Шредингера, учитывающему значение (1):'
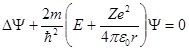 , (2)
, (2)
где m – масса электрона, Е – полная энергия электрона в атоме.
Это так называемое стационарное уравнение Шрёдингера для электрона водородоподобного атома ВДПА.
1. Энергия.В теории дифференциальных уравнений доказывается, что уравнения типа (2) имеют решения, удовлетворяющие требованиям однозначности, конечности и непрерывности волновой функции Ψ, только при собственных значениях энергии
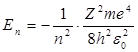 (n = 1, 2, 3,…), (3)
(n = 1, 2, 3,…), (3)
т. е. для дискретною набора отрицательных значений энергии.
Таким образом, как и в случае «потенциальной ямы» с бесконечно высокими «стенками» , решение уравнения Шредингера для атома водорода приводит к появлению дискретных энергетических уровней. Возможные значения Е1, Е2, Е3, ... показаны па рис. 6 в виде горизонтальных прямых. Самый нижний уровень Е1, отвечающий минимальной возможной энергии, – основной,все остальные (Еn>E1, n = 2, 3,…) – возбужденные. При Е < 0 движение электрона является связаннымон находится внутри гиперболической «потенциальной ямы». Из рисунка следует, что по мере роста главного квантового числа п энергетические уровни располагаются теснее и при п=∞ Е∞= 0. При Е > 0 движение электрона является свободным;область непрерывного спектра Е >0 (заштрихована на рис. 6) соответствует ионизованному атому.Энергия ионизации атома водорода равна
Ei = - E1 = me4 / (8h2ε02) = 13,55 эВ.
2. Квантовые числа.В квантовой механике доказывается, что уравнению Шредингера (2) удовлетворяют собственные функции 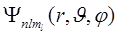 , определяемые тремя квантовыми числами: главным п, орбитальным l и магнитным ml.
, определяемые тремя квантовыми числами: главным п, орбитальным l и магнитным ml.
Главное квантовое число n,согласно (3), определяет энергетические уровни электрона в атоме и может принимать любые целочисленные значения, начиная с единицы:
n =1, 2. 3, ....
Из решения уравнения Шредингера вытекает, что момент импульса (механический и орбитальный момент) электрона квантуется, т. е. не может быть произвольным, а принимает дискретные значения, определяемые формулой
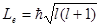 , (4)
, (4)
где l – орбитальное квантовое число,которое при заданном n принимает значения
l = 0, 1, ...,(n - 1), (5)
т. е. всего п значений, и определяет момент импульса электронав атоме.
Из решения уравнений Шредингера следует также, что вектор Leмомента импульса электрона может иметь лишь такие ориентации в пространстве, при которых его проекция Lеz на направление z внешнего магнитного поля принимает квантованные значения, кратные ħ
Lez = ħml, (223.6)
где тl – магнитное квантовое число,которое при заданном l может принимать значения
ml = 0, ±1, ±2, ..., ± l, (223.7)
т.е. всего 2l+1 значений. Таким образом, магнитное квантовое числотl определяет проекцию момента импульса электрона на заданное направление,причем вектор момента импульса электрона в атоме может иметь в пространстве 2l + 1 ориентаций.
Наличие квантового числа ml должно привести в магнитном поле к расщеплению уровня с главным квантовым числом n на 2l+1подуровней. Соответственно в спектре атома должно наблюдаться расщепление спектральных линий. Действительно, расщепление энергетических уровней и магнитном поле было обнаружено в 1896 г, голландским физиком П. Зееманом (1865 - 1945) и получило название аффекта Зеемана.Расщепление уровней энергии во внешнем электрическом поле, тоже доказанное экспериментально, называется эффектом Штарка .
Хотя энергия электрона (3) и зависит только от главного квантового числа n, но каждому собственному значению Еп (кроме Е1) соответствует несколько собственных функций 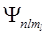 , отличающихся значениями l и ml. Следовательно, атом водорода может иметь одно и то же значение энергии, находясь в нескольких различных состояниях. Так как при данном п орбитальное квантовое число l может изменяться от 0 до n – 1, (см. (5)), а каждому значению l соответствует 2l + 1 различных значений тl (7), то число различных состояний, соответствующих данному п, равно
, отличающихся значениями l и ml. Следовательно, атом водорода может иметь одно и то же значение энергии, находясь в нескольких различных состояниях. Так как при данном п орбитальное квантовое число l может изменяться от 0 до n – 1, (см. (5)), а каждому значению l соответствует 2l + 1 различных значений тl (7), то число различных состояний, соответствующих данному п, равно
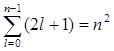 . (8)
. (8)
Квантовые числа и их значения являются следствием решений уравнений Шредингера и условий однозначности, непрерывности и конечности, налагаемых на волновую функцию Ψ.
Вероятность обнаружения электрона в различных частях атома различна. Электрон при своем движении как бы «размазан» по всему объему, образуя электронное облако, плотность (густота) которого характеризует вероятность нахождения электрона в различных точках объема атома. Квантовые числа п и l характеризуют размер и форму электронного облака, а квантовое число тl характеризует ориентацию электронного облака в пространстве.
В атомной физике, по аналогии со спектроскопией, состояние электрона, характеризующееся квантовыми числами l = 0, называют s – состоянием (электрон в этом состоянии называют s – электроном), l = 1 — р-состоянием, l = 2— d-состоянием, l = 3 — f-состоянием и т.д. Значение главного квантового числа указывается перед условным обозначением орбитального квантового числа (см. рис. 8). Например, электроны в состояниях с n = 2 и l = 0 и 1 обозначаются соответственно символами 2s и 2р.
На рис. 7 для примера приведено распределение электронной плотности (формы электронного облака) для состояний атома водорода при п = 1 и n =2, определяемое | 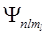 |2. Как видно из рисунка, оно зависит от п, l и тl. Так, при l = 0 электронная плотность отлична от нуля в центре и не зависит от направления (сферически-симметрична), а для остальных состояний в центре равна нулю и зависит от направления.
|2. Как видно из рисунка, оно зависит от п, l и тl. Так, при l = 0 электронная плотность отлична от нуля в центре и не зависит от направления (сферически-симметрична), а для остальных состояний в центре равна нулю и зависит от направления.
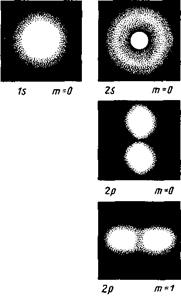
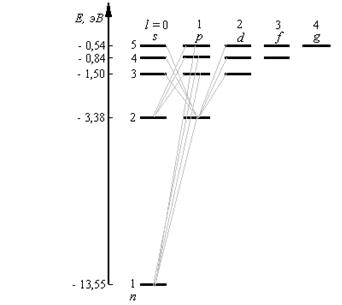
Рис. 7 Рис. 8
§ 3.2.2. Спин электрона. Спиновое квантовое число
О. Штерном и В. Герлахом были поставлены опыты (1921), целью которых являлось измерение магнитных моментов рm атомов различных химических элементов. Для определения орбитального момента импульса Ll и рm одного электрона опыты должны быть поставлены с атомами, у которых орбитальные механические (и магнитные) моменты всех электронов, кроме одного, взаимно компенсируют друг друга. Такими атомами являются атомы химических элементов, образующие первую группу периодической системы Менделеева и имеющие один валентный электрон на внешней оболочке.
Идея опытов Штерна и Герлаха заключалась в измерении силы, действующей на атом в неоднородном магнитном поле. В таком магнитном поле на атом должна действовать сила
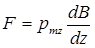 , (1)
, (1)
где В – индукция магнитного поля (направленная вдоль оси z), неоднородного только вдоль этой же оси.
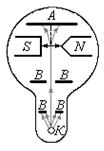

Рис. 9 Рис. 10
Опыты Штерна и Герлаха обнаружили ошибочность классического предположения отом, что магнитный момент рm и механический момент импульса Ll атома произвольно ориентируются относительно направления внешнего поля, и подтвердили наличие пространcтвенного квантования. Схема первых опытов Штерна и Герлаха изображена на рис. 9.
В трубке, где был создан вакуум порядка 10 -5 мм рт. ст., помещался источник пучка атомов — нагреваемый до высокой температуры серебряный шарик К. Атомы серебра вылетали с его поверхности со средней тепловой скоростью порядка 100 м/с, соответствующей температуре испарения серебра. Из этих атомов при помощи щелевых диафрагм В вырезался узкий пучок, проходящий через сильное и неоднородное магнитное поле, направленное перпендикулярно пучку. Основная трудность опыта состояла в том, чтобы достигнуть такой большой неоднородности магнитного поля, которая сказывалась бы на расстояниях порядка размеров атома. При такой величине неоднородности поля, как показывает формула (39.17), можно было рассчитывать получить значительную отклоняющую силу F, действующую на атом в магнитном поле. Необходимая неоднородность поля была достигнута в результате применения сильного электромагнита SN с полюсными наконечниками специальной формы. Приемником атомов серебра служила фотопластинка А.
Если бы момент импульса Ll атома (и его магнитный момент рm ) мог принимать произвольные ориентации в магнитном поле, то можно было бы ожидать непрерывного распределения попаданий атомов на пластинку с большей плотностью попаданий в середине пластинки и меньшей плотностью к ее краям. Опыты, проведенные с серебром и атомами других элементов периодической системы, привели к совершенно другому результату. На рис. 10 показана фотография результата опыта Штерна и Герлаха с литием. Из рисунка видно, что на фотопластинке получились две резкие полосы — все атомы отклонялись в магнитном поле двояко, что соответствовало лишь двум возможным ориентациям магнитного момента во внешнем поле. Момент импульса атома (и его магнитный момент) равен суммарным моментам электронов, поскольку магнитные моменты ядер имеют значительно меньшее значение, чем магнитные моменты электронов. Последние совпадают с суммарными моментами валентных электронов, так как моменты электронов замкнутых оболочек компенсируются.
У лития и других атомов первой группы периодической системы имеется один валентный оптический электрон (s-состояние). Таким образом, моменты импульса и магнитные моменты таких атомов совпадают с моментами электрона.
Таким образом, опыты Штерна и Герлаха не только подтвердили пространственное квантование моментов импульса в магнитном поле, но, кроме того, экспериментально подтвердили вывод о том, что магнитные моменты электронов и атомов состоят из некоторого числа «элементарных моментов», т, е. имеют дискретную природу, связанную с квантованием момента импульса.
О. Штерн и В. Герлах, проводя прямые измерения магнитных моментов, обнаружили, что узкий пучок атомов водорода, заведомо находящихся в s-состоянии, в неоднородном магнитном поле расщепляется на два пучка. В этом состоянии момент импульса электрона равен нулю (l = 0, ml = 0)). Магнитный момент атома, связанный с орбитальным движением электрона, пропорционален механическому моменту, поэтому он равен нулю, и магнитное поле не должно оказывать влияния на движение атомов водорода в основном состоянии, т. е. расщепления быть не должно. Однако в дальнейшем при применении спектральных приборов с большой разрешающей способностью было доказано, что спектральные линии атома водорода обнаруживают тонкую структуру (являются дублетами) даже в отсутствие магнитного поля.
Для объяснения этого американские физики Д. Уленбек (1900- 1974) и С. Гаудсмит (1902-1979) предположили, что электрон обладает собственным неуничтожимым механическим моментом импульса,не связанным с движением электрона в пространстве — спином.
Спин электрона (и всех других микрочастиц) — квантовая величина, у нее нет классического аналога; это внутреннее неотъемлемое свойство электрона, подобное его заряду и массе.
Если электрону приписывается собственный механический момент импульса (спин) Ls, то ему соответствует собственный (спиновый) магнитный момент рms,. Согласно общим выводам квантовой механики, спин квантуется по закону
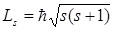 ,
,
гдеs – спиновое квантовое число.
По аналогии с орбитальным моментом импульса, проекция Lsz, спина квантуется так, что вектор Ls, может принимать 2s + 1 ориентаций. Так как в опытах Штерна и Герлаха наблюдались только две ориентации, то 2s + 1 = 2, откуда s = 1 / 2. Проекция спина на направление внешнего магнитного поля, являясь квантованной величиной, определяется выражением
Lsz = ħms,
гдеms – магнитное спиновое квантовое число; оно может иметь только два значения: ms = ± ½.
Таким образом, опытные данные привели к необходимости характеризовать электроны (и микрочастицы вообще) добавочной внутренней степенью свободы. Поэтому для полного описания состоянии электрона в атоме необходимо наряду с главным, орбитальным и магнитным квантовыми числами задавать еще магнитное спиновое квантовое число.
Магнитные моменты электрона и их проекции на направление внешнего магнитного поля:
Модуль магнитного момента электрона
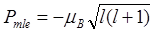 .
.
Проекция магнитного момента электрона
Pmlez = μB ml (ml = -l, -l + 1,…, l –1, l).
Модуль собственного (спинового) магнитного момента электрона
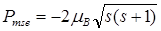 .
.
Проекция собственного (спинового) магнитного момента электрона
Pmsez = ± μB.
Полный момент импульса электрона (слагается из двух: орбитального Lle и спинового Lse)
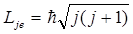 , (j = l + s, l + s – 1, … , |l - s|).
, (j = l + s, l + s – 1, … , |l - s|).
Проекция полного момента импульса электрона
Ljez = ħmj, (mj = -j, -j + 1, …, j – 1, j).
Полный магнитный момент электрона
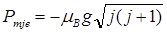 , где
, где 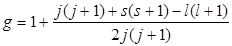 (множитель Ландо).
(множитель Ландо).
Проекция полного магнитного момента электрона
Pmjez = -μB g mj , (mj = -j, -j + 1, …, j – 1, j).
Связь между орбитальными магнитным и механическим моментами электрона определяется выражением 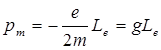 , где
, где 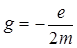 –-гиромагнитное отношение орбитальных моментов.
–-гиромагнитное отношение орбитальных моментов.
Связь между спиновыми магнитным и механическим моментами электрона определяется выражением 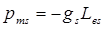 , где
, где 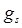 –-гиромагнитное отношение спиновых моментов.
–-гиромагнитное отношение спиновых моментов.
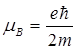 –- магнетон Бора, являющийся единицей магнитного момента электрона.
–- магнетон Бора, являющийся единицей магнитного момента электрона.
Дата добавления: 2015-08-08; просмотров: 4093;
