АТОМЕ ВОДОРОДА
Основные особенности квантовой модели атома водорода можно уяснить, сопоставляя его характеристики (W, 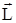 , Lz), выраженные через квантовые числа (n, l, ml), с распределением в пространстве вероятности обнаружения электрона вблизи ядра. Электрон при своем движении как бы “размазан” по некоторому объему, образуя электронное облако с распределенным зарядом, объемная плотность r которого характеризует различную вероятность нахождения электрона в той или иной точке пространства:
, Lz), выраженные через квантовые числа (n, l, ml), с распределением в пространстве вероятности обнаружения электрона вблизи ядра. Электрон при своем движении как бы “размазан” по некоторому объему, образуя электронное облако с распределенным зарядом, объемная плотность r которого характеризует различную вероятность нахождения электрона в той или иной точке пространства:
 ,
,
где е – заряд электрона, 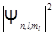 - квадрат модуля волновой функции
- квадрат модуля волновой функции
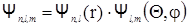 . (2.73)
. (2.73)
Квантовые числа n и l характеризуют размер и форму электронного облака, а число mе – его ориентацию в пространстве.
Для обозначения и записи электронных состояний с разными значениями орбитального квантового числа l используют символику, приведенную в таблице 1.
Таблица 1.
| Значение l | ||||||
| Обозначение состояния | s | Р | d | f | q | h |
Как следует из решения уравнения Шредингера, волновые функции, соответствующие s – состояниям являются сферически-симметричными. Это значит, что вероятность обнаружить электрон на некотором расстоянии от ядра зависит лишь от этого расстояния и не зависит от углов Q и j. Например, в состоянии с минимальной энергией W1 (основное, или 1s-состояние, соответствующее значениям n=1, l =0,ml=0) волновая функция электрона имеет вид простой экспоненты: 
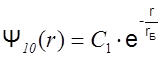 ,
,
где rБ - боровский радиус (rБ =0,528·10-10 м), С1 нормировочный множитель. 
|
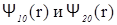 представлены на рис. 2.16.
представлены на рис. 2.16.
Рис.2.16
Более выразительным является радиальное распределение вероятности dPs встретить электрон в сферическом слое радиуса r, толщиной dr (см. рис. 2.17,а):
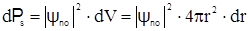 ,
,
где dV - объем сферического слоя.
 | |||
 | |||
а) б)
Рис.2.17
Графики распределения dPs\dr для состояний 1s, 2s и 3s изображены на рис.2.17,б на фоне графика кулоновской потенциальной энергии. Видно, что с наибольшей вероятностью электрон атома водорода в 1s - состоянии посещает сферический слой радиуса rБ (радиус первой боровской орбиты). Следовательно, в нормальном состоянии атома водорода его электрон представляет собой сферическое облако отрицательного заряда, имеющего максимальную плотность r вблизи расстояния r = rБ . Непосредственно около ядра (r = 0) и на большом расстоянии от него r стремится к нулю. В возбужденных состояниях s- электрон может находиться в сферических слоях I и II (для 2s-состояния) и I, II, III (для 3s-состояния), разделенных узловыми поверхностями, на которых dPs=0 (точки А и B на рис.2.17,б). Основное время 2s-электрон проводит в слое II, а 3s-электрон – в слое III, то есть на все большем расстоянии r от ядра. В связи с этим, размер атома водорода растет с ростом энергии (с ростом числа n). Электронные облака 4s, 5s и т.д. состояний тоже сферически симметричны, но простираются на все большие расстояния и имеют все больше число NS узловых поверхностей (NS = n–1).
Радиальные распределения вероятности dPs/dr для р-состояний характеризуются наличием (n-2) узловых поверхностей, поэтому 2р-состояние (n=2) узловых поверхностей не имеет.
Форма электронных облаков для р-, d-, f- (и т.д.) состояний является более сложной, поскольку в этом случае вероятность пребывания электрона в той или иной точке пространства зависит не только от r, но и от угла Q между радиус-вектором r и соответствующей осью координат (см.рис.2.14), что учтено множителем 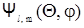 в формуле (2.73).
в формуле (2.73).
Ориентация электронных облаков в пространстве зависит от значения магнитного квантового числа ml, то есть от проекции момента импульса электрона.
На рис. 2.18 схематично отображены векторные диаграммы для различных состояний электрона, дающие представление о форме электронных облаков возбужденного атома водорода. Следует лишь резкие границы “гантелей” или “розеток” представить размытыми.
Таким образом, квантовая теория отказывается от классических представлений об электронных орбитах: вероятность обнаружения электрона в различных частях атома различна, однако можно указать точки, соответствующие максимальному значению плотности вероятности нахождения электрона в атоме.
 2р-состояние
(l=1) 2р-состояние
(l=1)
| |
| 3d-состояние (l=2) |
Рис.2.18
Дата добавления: 2015-07-24; просмотров: 1049;
