Квантовое явление прохождения частицы через области пространства, запрещенные законами классической физики, называется туннельным эффектом.

Существование этого явления следует непосредственно из решения уравнения Шредингера.

Рассмотрим идеализированный потенциальный барьер прямоугольной формы (рис. 2.9).

Рис.2.8 Рис. 2.9

В данном случае потенциальная энергия частицы W_p(x) равна нулю всюду, кроме области 0<x<d (d - ширина барьера), где W_p(x) имеет постоянное значение W_pm– высота барьера. Таким образом

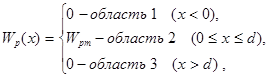(2.47)

Предположим, что микрочастица движется к барьеру из области х < 0

Обозначим волновые функции микрочастицы для указанных областей, соответственно, y₁,y₂, и y₃. Тогда уравнение Шредингера (2.29) с учетом (2.47) примет вид:

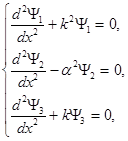(2.48)

где k² = 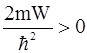, 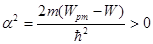. (2.49)

Решением уравнений (2.48) будут функции:

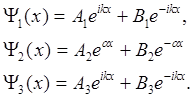, (2.50)

В формулах (2.50) слагаемое вида 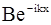- это плоская волна де Бройля, распространяющаяся в отрицательном направлении оси х: в области 1 она соответствует частице, отраженной барьера. Поскольку в области 3 (за барьером) будет только проходящая волна (слагаемое A₃ 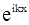), то амплитуда В₃ = 0. Чтобы выполнить условие конечности y - функции при любых А₂, нужно принять равным нулю коэффициент A₂.

Таким образом, с учетом значений В₃ = 0, А₂ = 0, уравнения (2.50) примут вид

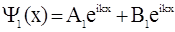(для области 1) ,

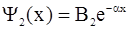(для области 2) , (2.51)

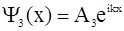(для области 3).

Соотношения (2.51) показывают, что волновая функция микрочастицы внутри барьера (область 2) не равна нулю, а убывает экспоненциально;

- в области 3 (за барьером) волновая функция имеет вид волны де Бройля с той же длиной 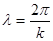, что и в области 1, но с меньшей амплитудой ( А₃ < А₁).

На рисунке 2.10 изображены:

- действительная часть волновой функции y₁(х) в области 1 при отсутствии отражения на границе областей 1 и 2 (В₁ = 0): RеY₁ = А ₁ соs kх;

- функция, экспоненциально убывающая в области 2: ;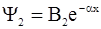

- действительная часть волновой функции Y₃ в области 3: .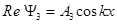

и

Рис.2.10

Следовательно микрочастица имеет отличную от нуля вероятность просачивания сквозь потенциальный барьер конечной ширины d.

Эта вероятность определяется отношением квадратов модулей амплитуд прошедшей и падающей волн и называется коэффициентом прозрачности барьера.

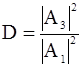. (2.52)

Величина

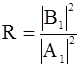=1– D (2.53)

определяет вероятность отражения микрочастицы от потенциального барьера и называется коэффициентом отражения. По квантовой теории (в отличие от классической) имеется некоторая вероятность отражения даже в случае, если W>W_pm - надбарьерное отражение.

Для нахождения неизвестных амплитуд ( А₁, В₁, В_2, А₃ ), входящих в уравнения (2.51) и в соотношения (2.52) и (2.53), используют свойство непрерывности Y-функции и ее первой пространственной производной 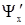(x) на границах барьера:

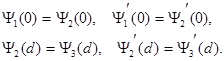(2.54)

Решение уравнений (2.51) с учетом граничных условий (2.54), позволяет выразить коэффициент прозрачности (2.52) через высоту и ширину барьера

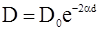, (2.55)

где 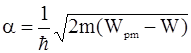в соответствии с формулой (2.49), а .

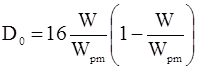Увеличение массы m частицы, ширины барьера d и его высоты (дефицита энергии (W_pm –W)) уменьшает коэффициент прозрачности: вероятность туннельного эффекта уменьшается.

В пределе ( 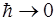) получаем результат классической механики:

D®0, R®1.

Туннельный эффект (подбарьерное прохождение), как и надбарьерное отражение – это специфические квантовые явления, объяснимые на основе принципа неопределенности. Дело в том, что в квантовой механике полную энергию W частицы нельзя представить в виде суммы кинетической энергии – функции импульса ( 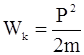) и потенциальной энергии – функции координат ( 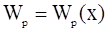). Эту возможность исключает соотношение 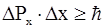: если зафиксировать частицу в определенной области Dx, то есть задать ее потенциальную энергию W_Р(х), то вносится неопределенность в ее импульс и, следовательно, в кинетическую энергию W_k(P). Таким образом, хотя полная энергия W имеет определенное значение, она не может быть представлена в виде суммы точно заданных энергий W_p и W_k.

Явление прохождения частицы сквозь потенциальный барьер существенно для понимания таких явлений, как холодная эмиссия электронов из металла, контактная разность потенциалов, альфа- распад радиоактивных ядер, термоядерные реакции; на туннельном эффекте основан принцип действия туннельных диодов.