НЕСТАЦИОНАРНОЕ УРАВНЕНИЕ ШРЕДИНГЕРА

Основное уравнение (закон) нерелятивистской квантовой механики впервые сформулировал Э. Шредингер в 1926 году. Оно играет в квантовой механике такую же важную роль, как и уравнение второго закона Ньютона в классической механике.

Для микрочастицы массой m, движущейся в некотором силовом поле, нестационарное (временное) уравнение Шредингера имеет вид:

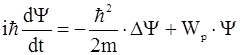, (2.24)

где y = y |x, y, z, t|- искомая волновая функция микрочастицы,

i= 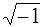-мнимая единица,

D - оператор Лапласа: ,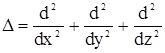

W_p- потенциальная функция частицы.

В том случае, когда W_p не зависит явно от времени, W_p имеет смысл потенциальной энергии частицы в силовом поле.

Уравнение (2.24) можно записать в более компактной символической форме

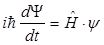, (2.25)

где 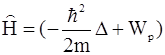- оператор полной энергии – оператор Гамильтона (или гамильтониан).

Для решения уравнения Шредингера, то есть для отыскания y -функции, необходимо задать начальные временные условия, а также условия, определяющие движение частицы на границах рассматриваемого силового поля. Сама же волновая функция, описывающая реализуемые состояния микрочастицы, должна удовлетворять общим ограничительным условиям, сформулированным ранее (п. 2.3.1).

Доказательством правильности уравнения Шредингера является согласие с опытом тех выводов, к которым оно приводит.