Неопределенность значений сопряженных параметров обусловлена не методами или средствами измерения, а двойственной, корпускулярно-волновой природой микрообъектов.

Если мы будем стремиться поточнее определить координату х микрочастицы, то есть уменьшать Dх, то неопределенность проекции ее импульса, т.е.DR_x, увеличивается, и наоборот.

Справедливость соотношений (2.18) можно проиллюстрировать следующим примером.

Пусть поток электронов, имеющих импульс 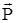, проходит через узкую щель, расположенную перпендикулярно их движению. Если размер щели D х соизмерим с длинной волны де Бройля 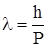для электронов, то будет наблюдаться дифракция (рис.2.3) .

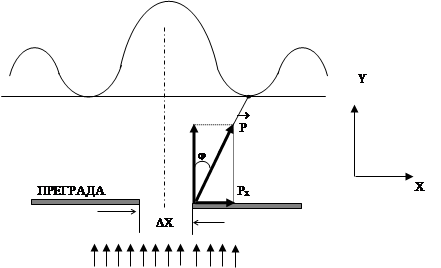Рис. 2.3

До преграды электроны движутся вдоль оси U, поэтому составляющая импульса Р_х = 0, так что DP_x = 0, а координата х совершенно неопределенна (Dx®¥).

В момент прохождения через щель положение частиц вдоль оси Х определяется с точностью до ширины щели, т.е. с неопределенностью Dх, но из-за дифракции часть электронов будет отклоняться от первоначального направления, приобретая составляющую импульса в направлении оси Х.

Для электронов, попавших в пределы главного (центрального) максимума, неопределенность импульса DР_х будет соизмерима с величиной импульса, то есть

, (2.20)

где j - угол, соответствующий первому дифракционному минимуму (рис.2.3).

Первый дифракционный минимум наблюдается при условии

Dx×sinj=l. (2.21)

Подставляя (2.21) в (2.20), получим

Dx×DR_х=h. (2.22)

Поскольку для некоторой части электронов (тех, которые попали за пределы центрального максимума) величина DR_x>Rsinj, то Dx×DR_х³h, то есть по порядку величины больше .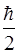

Соотношение (2.22) получено при одновременном использовании классических характеристик движения частицы (координаты, импульса) с учетом наличия у нее волновых свойств. Строгий вывод дает соотношения неопределенностей для координат и импульсов в виде неравенств (2.18).

С помощью принципа неопределенности можно объяснить многие наблюдаемые явления и факты: устойчивость атомов и молекул, свойства, (жидкого) гелия, структуру и размеры атомных ядер, a -распад и т.д.

В частности, соотношение неопределенности (2.19) позволяет понять наблюдаемую на опыте размытость спектральных линий: возбужденное состояние атома имеет конечное время жизни D t, а значит характеризуется неопределенностью энергии 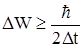, поэтому частота излученного фотона тоже будет иметь разброс (неопределенность)

.

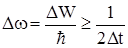Измеряя ширину спектральной линии, можно оценить порядок среднего времени существования атома в возбужденном квантовом состоянии.

С увеличением массы m микрообъекта ограничения, вносимые в возможность применения классических понятий, уменьшаются. Действительно, поскольку Dр =mD 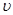, то из соотношения (2.18) следует, что

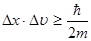, (2.23)

то есть, чем больше масса m объекта, тем меньше произведение неопределенностей его координаты и скорости, и тем с большей точностью можно применять к такому объекту понятие траектории.

Например, для пылинки массой m=10^-13 кг с линейным размером d=1мкм = 10^-6м, координата которой определена с точностью до 0,01d, (т.е. Dх~10^-8м), неопределенность скорости, согласно (2.23) , составляет

.

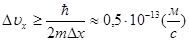Такая неопределенность незначительна при всех скоростях, допустимых для пылинки. Значит, такой объект можно рассматривать как классическую частицу, движущуюся по определенной траектории. Формально для таких тел постоянную Планка в формулах (2.18), (2,19), (2.23) можно считать пренебрежимо малой (h® 0). При этом условии квантовые свойства микрообъектов оказываются несущественными. Это, например, имеет место при движении электрона в электронно-лучевой трубке. Если электроны движутся к экрану трубки со скоростью 10⁷ м/с, измеренной с точностью до 0,01%, т.е.u =10³ м/с, то неопределенность (размытие) координаты электрона составляет

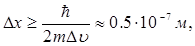
что мало по сравнению с размерами пятна на экране трубки. Значит, учет соотношения неопределенностей в этом случае необязателен.

Что касается электрона, движущегося в каком-либо атоме, то его координаты можно определить лишь с точностью до размеров атома, то есть, Dх ~ 10^-10м. Тогда, согласно (2.23), неопределенность скорости электрона оказывается такого же порядка, что и сама скорость: 10⁶ м/с. Следовательно, при движении электрона вокруг ядра нельзя использовать понятие траектории (или орбиты), а можно говорить лишь о локализации электрона в пределах атома в целом. Таким образом, соотношение неопределенностей является квантовым ограничением применимости классической механики к микрообъектам.

Важно понять, что соотношение неопределенностей не ставит никаких ограничений на возможность познания природы (как утверждали в свое время философы-идеалисты), - оно лишь показывает область применимости классических представлений.