ВОЛНОВАЯ ФУНКЦИЯ
На первом этапе развития квантовой механики возникла проблема физической природы волн де Бройля.
Дифракционная картина, наблюдаемая в опытах с микрочастицами, свидетельствует о неодинаковом распределении потоков этих частиц, отраженных (или рассеянных) по разным направлениям: в некоторых направлениях наблюдается большее число частиц, чем в других. С позицией волновой теории это означает, что таким направлениям соответствует наибольшая интенсивность волн де Бройля. Очевидно, в дифракционной картине для микрочастиц проявляется статистическая (вероятностная) закономерность: частицы с большей вероятностью попадают в те области пространства, где интенсивность волн де Бройля больше.
Таким образом, своеобразные волновые свойства микрочастицы можно объяснить, предположив, что интенсивность волны де Бройля является мерой вероятности нахождения частицы в конкретных условиях, т.е. в определенном квантовом состоянии.
Для характеристики состояния микрочастицы в квантовой механике вводится волновая функция [¦1] [¦2] y(x, y, z, t). Ее статистическую интерпретацию дал впервые в 1926 г. М.Борн.
Если рассмотреть бесконечно малый объем dV=dx×dy×dz вблизи точки с координатами x,y,z, то вероятность нахождения частицы в момент времени t внутри этого объема дается выражением
dР= 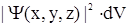 . (2.14)
. (2.14)
y - функция может быть и комплексной величиной, поэтому
|y|2=y×y*,
где y* - функция, комплексно сопряженная с y.
Свое название волновая функция получила потому, что ее математическое выражение для свободной частицы похоже на выражение, описывающее волну. Физический смысл имеет не сама y - функция, а квадрат ее модуля, который определяет интенсивность волны де Бройля микрообъекта. Как следует из (2.14), квадрат модуля волновой функции
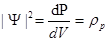 (2.15)
(2.15)
имеет смысл плотности вероятностиrp(x, y, z, t)обнаружить частицу в окрестности точки х, у, z в момент времени t.
В соответствии со своим математическим смыслом вероятность должна быть нормирована на единицу (вероятность достоверного события), т.е. 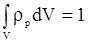 , откуда следует условие нормировки для волновой функции:
, откуда следует условие нормировки для волновой функции:
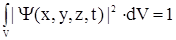 . (2.16)
. (2.16)
Интегрирование в (2.16) осуществляется по всему объему V, доступному для движения микрочастицы, т.е. по координатам х, y, z от -¥ до +¥.
Кроме условия нормировки (2.16) y - функция должна удовлетворять ряду ограничительных условий:
1) y - функция должна быть конечной, однозначной, непрерывной (поскольку вероятность не может меняться скачком);
2) производные от y - функции по координатам и времени должны быть непрерывны;
3) y- функция должна удовлетворять принципу суперпозиции: если в данных условиях система может находиться в различных состояниях, описываемых волновыми функциями y1, y2, ... yn, то в этих же условиях возможны состояния с волновой функцией y, являющейся линейной комбинацией yi , то есть 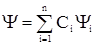 ,
,
где Сn (n = 1,2,3…) – произвольные комплексные числа.
Волновая функция является основным носителем информации о волновых и корпускулярных свойствах микрообъектов.С ее помощью в квантовоймеханике вычисляют средние значения физических величин, характеризующих данный микрообъект. Например, среднее расстояние < r > электрона от ядра можно найти по формуле
<r>= 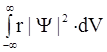 .
.
Дата добавления: 2015-07-24; просмотров: 935;
