Волновая функция. Уравнение Шредингера.

Физикой микрочастиц, учитывая волновые свойства, является квантовая механика. Особенностью квантовой механики является использование вероятностного подхода к описанию микрочастиц. Состояние микрочастиц должно описываться волновой функцией, связанной с вероятностью. Т.к. функция меняется по волновому закону, т.е. принимает положительные и отрицательные значения, она сама не может быть вероятностью. Бором было установлено, что механическим смыслом обладает не сама эта функция, а её квадрат. Эту функцию назвали волновой или ψ функцией. 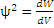– плотность вероятности, т.е. соотношение вероятности dW того, что частица находится в объёме dV=dxdydz к величине этого объёма.

Если известен 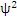, то легко вычислить радиус орбиты электрона в атоме 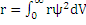. Функция 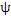должна быть конечной, однозначной и непрерывной. Она удовлетворяет условию нормировки.

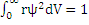- т.е. вероятность нахождения частицы в пространстве =1.

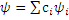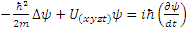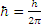Все ψ удовлетворяют принципу суперпозиции, т.е. если она может находиться в некоторых состояниях ψ₁, ψ₂…, то возможно также состояние ψ, которое является линейной комбинацией этого состояния , где C_i – весовые коэффициенты. Уравнение, решением которого является вид функции ψ, постулировано Шлебенсором в 1926: , где , m – масса; - оператор Лапласа; U_(xyzt) – потенциальная энергия микрочастицы в внешнем поле.

Для стационарного случая, когда U_(xyzt) не зависит от времени, функцию ψ_(xyz) можно записать , . => .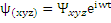

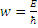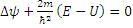В общем виде оно не решается. Конкретный вид его определяется начальными граничными условиями. Решение существует только для определённых E, т.е. такая частица имеет дискретный спектр.