КВАНТОВЫЕ ЧИСЛА

Потенциальная энергия электростатического взаимодействия электрона и протона (ядра атома водорода) зависит только от расстояния r между ними:

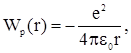(2.64)

где е – заряд электрона.

С учетом (2.64) уравнение Шредингера для стационарного состояния атома водорода имеет вид:

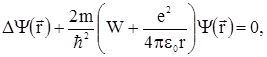(2.65)

где 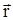= 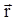(x, y, z), причем = .

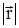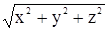Функцию (2.64) можно представить графически в виде кулоновской потенциальной ямы, сечение которой изображено на рис.2.13.

Рис.2.13

Поскольку поле сферически симметрично, то уравнение (2.65) лучше записать в сферических координатах с центром на ядре (рис.2.14). Они связаны с декартовыми координатами соотношениями:

х = r×sinQ×cosj,

y = r×sinQ×sinj,

z = r×cosQ,

где Q - полярный угол,

j - азимутальный угол.

Рис.2.14

Выразить оператор Лапласа D в сферических координатах довольно просто, но нужно выполнить громоздкие выкладки, поэтому запишем сразу окончательный результат:

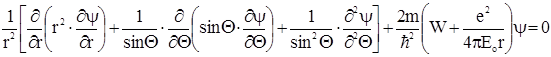(2.66)

Это уравнение имеет физически осмысленные решения, удовлетворяющие требованиям однозначности, конечности и непрерывности волновой функции в двух случаях:

- при любых положительных значениях полной энергии (W>0) электрона, что соответствует свободному состоянию электрона (ионизация атома) – заштрихованная область на рис.2.13.

- при дискретных отрицательных значениях полной энергии (W_n<0), соответствующих связанному состоянию электрона в потенциальном поле ядра, причем

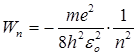, (2.67)

где n = 1,2,3,… - главное квантовое число.

С ростом числа n энергетические уровни дискретного спектра сгущаются; предельному значению n соответствует энергия W_¥=0, отделяющая дискретный спектр от непрерывного (см.рис.2.13).

Выражение (2.67) совпадает с формулой (2.8), полученной Н.Бором

(см. п 2.1.3). Однако, в квантовой механике дискретность энергии не постулируется, а следует непосредственно из решения уравнения (2.66). Вследствие трехмерного характера задачи волновая функция электрона в этом уравнении в общем случае будет зависеть от всех трех координат, то есть y = ψ(r, Q, j), поэтому квантовые состояния электрона имеющие физический смысл , будут определяться не одним, а тремя квантовыми числами: главным –n, орбитальным – l и магнитным – m_е.

Главное квантовое число определяет энергию электрона в соответствующем состоянии атома водорода согласно формуле (2.67).

Для любого n дифференциальное уравнение (2.66) имеет n линейно независимых решений (n волновых функций), которые можно классифицировать с помощью квантового числа l .

Орбитальное квантовое число l определяет модуль вектора механического орбитального момента импульса 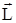электрона в атоме:

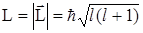. (2.68)

Число l характеризует пространственную симметрию волновой функции электрона. Например, все ψ - функции, соответствующие значению l = 0, сферически симметричны. При данном n число l может принимать значения от 0 до (n – 1), то есть всего n значений:

l = 0,1,2,…,(n –1). (2.69)

Для каждой пары чисел (n, l) уравнение (2.66) имеет (2l+1) линейно независимых решений, которые классифицируются с помощью магнитного квантового числа m_е.

Магнитное орбитальное квантовое число m_l определяет разрешенные значения проекции вектора 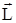на выделенное направление Z в пространстве (например, на направление магнитного поля):

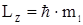. (2.70)

Зависимость ψ - функции от числа m_l возникает, если, например, атом находится во внешнем магнитном поле или, если магнитное поле порождается движением ядра и остальных электронов (в водородоподобном атоме).

Магнитное квантовое число принимает следующие значения:

m_l =0, ±1, ±2, ±3, …, ±l, (2.71)

поэтому угол между осью Z и вектором орбитального момента 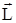может принимать лишь определенные величины и никогда не бывает равным нулю (всегда )

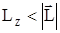Например, если l = 2, то L = 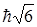, то проекция 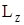может иметь пять дискретных значений: (-2 , - , 0, + , +2 ) (см.рис.2.15).

Рис.2.15

Таким образом, атом водорода может иметь одно и то же значение энергии W_n, находясь в нескольких разных квантовых состояниях, отличающихся величиной и направлением момента импульса 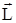электрона, то есть значениями квантовых чисел l и m_l. Эти состояния называются вырожденными. Число разных состояний для данного W называется кратностью g вырождения энергетического уровня:

g 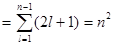. (2.72)