A, b –необязательны, если используются, то должны быть вещественными числами, причем a < b.

Рисунок 4. Решение уравнений средствами Mathcad
Приближенные значения корней (начальные приближения) могут быть:
1. Известны из физического смысла задачи.
2. Известны из решения аналогичной задачи при других исходных данных.
3. Найдены графическим способом.
Наиболее распространен графический способ определения начальных приближений. Принимая во внимание, что действительные корни уравнения f(x) = 0 - это точки пересечения графика функции f(x) с осью абсцисс, достаточно построить график функции f(x) и отметить точки пересечения f(x)с осью Ох, или отметить на оси Ох отрезки, содержащие по одному корню. Построение графиков часто удается сильно упростить, заменив уравнение f(x) = 0 равносильным ему уравнением: 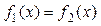 ,где функции f1(x) и f2(x) - более простые, чем функция f(x). Тогда, построив графики функций у = f1(x) и у = f2(x), искомые корни получим как абсциссы точек пересечения этих графиков.
,где функции f1(x) и f2(x) - более простые, чем функция f(x). Тогда, построив графики функций у = f1(x) и у = f2(x), искомые корни получим как абсциссы точек пересечения этих графиков.
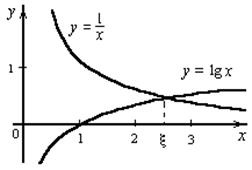
Пример. Графически отделить корни уравнения: x lg x = 1. Это уравнение удобно переписать в виде равенства: 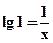
Отсюда ясно, что корни уравнения могут быть найдены как абсциссы точек пересечения логарифмической кривой y = lg x и гиперболы y = 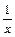 . Построив эти кривые, приближенно найдем единственный корень
. Построив эти кривые, приближенно найдем единственный корень 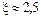 уравнения или определим его содержащий отрезок [2, 3].
уравнения или определим его содержащий отрезок [2, 3].
 |
Дата добавления: 2015-08-21; просмотров: 1656;
